Geoid Modelling for Surveying Works Using Satellite Geo-Spatial Data- Juniper Publishers

 Civil Engineering Research Journal- Juniper Publishers

 

Introduction

Nowadays fully three-dimensional positions - latitude, longitude and height are commonly provided by Global Positioning Systems (GPS) with WGS84 ellipsoid as a reference surface. The knowledge of terrain heights is very essential for several surveying and civil engineering works. The type of heights needed for such applications is a height above mean sea level (MSL), usually called orthometric height. A precise geoid model is required to transform GPS-based geodetic heights to orthometric height to allow such data to be directly used in surveying and civil engineering applications [1]. The process of geoid modelling can only be performed if dense networks of precise levelling or gravity and astronomical deflections of vertical are made available.

Objective

The objective of this article is to formulate a local geoid model that would allow utilization of GNSS data in the fields of surveying and civil engineering in Riyadh city, capital of Saudi Arabia.

Literature Review

Several regional or local geoid models have been developed, such as: Kamguia, et al [2] (Cameroon); Merry [3] (South Africa); Aleem KF [4] (Port Harcourt, Nigeria); Dawod & Hosny [5] (Egypt); Manandhar & Shanker [6] (Nepal); Younis [1] & [7] (Palestine). Developed and tested geoid models include: Milbert & Smith [8], developed a GEOID96 model for the United States and when testing 2729 GPS points on leveled benchmarks found a RMS error of 5.8cm with no offsets or trends removed. Zhan-Ji [9] showed that a geometric geoid model developed for Hong Kong would provide an accuracy of 3 cm and a relative geoid height difference less than 1 ppm for a base line longer than 30 km. Zan-Ji [10] constructed the Hong Kong gravimetric geoid with an accuracy of about 2 cm when compared with geoid heights of 31 check points derived from GPS/Leveling data. Lin 11], generated two geometric geoid models and one gravimetric-geometric geoid model for Tainan City using the GPS and leveling data. He used fifth- and seventh-degree polynomial, and achieved orthometric height accuracy of 2-4 cm.

Eteje [12] formed a geoid model using eight benchmarks. To interpolate geoid heights of new points, they used bi-cubic geoid model and obtained an accuracy of ± 1.7cm. Younis (7) constructed a geoid model for Palestine using finite element method. Using 2nd and 3rd order polynomial, the accuracy of 1-3 cm have been achieved. Kamguia, et al [2], formed a geometric geoid model for a small area in Cameroon and obtained an accuracy of 14 cm. After a four-parameter fitting to the GPS/levelled data, the accuracy reduced to 11 cm.

Geoid Modelling

There are two approaches for developing a geoid model: geometric and gravimetric approaches. Geometric is the one most applicable for surveying works of small extent, i. e. city extent or less. In this method, ellipsoidal heights h is measured by GNSS at points with known orthometric heights H. Then, the difference N (geoidal height) between h and H, known as geoidal height, is derived at all known points (N = h-H). Conversion between h and H at a point requires that N must be known at that point. Therefore, geoid modelling became an important problem in geodesy (Figure 1).

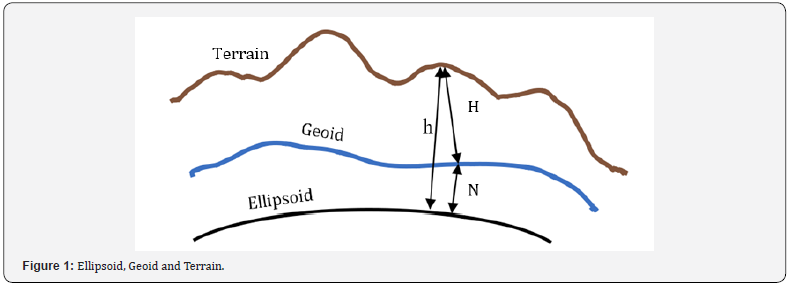
The simplest case of geometric geoid modelling is to consider that, the geoid and the ellipsoid are parallel. In this case we need a single control point to provide a constant height shift for all measured points in the vicinity. For more accuracy, we consider the geoid as a tilt plane. In this case, three control points are needed. But this consideration is still convenient only for a small area. The geoid is much more complex in shape. Therefore, more control points would be required to generate a reliable model by using one of the known numerical methods such as polynomials. In such approach, obtained geometric geoid model is a function of x and y (N= f (x, y)) is only valid over the area covered by the known control points. Hence, for small areas where sufficient control points are available the geometric approach is recommended to form a precise local geoid model [3]. Gravimetric approach, however, provides a uniform grid of geoidal heights over a large area, in contrast to the scattered point values over a limited area provided by the geometric method. However, it requires a complex numerical integration of gravity anomalies to determine a geoidal height.

The adopted model

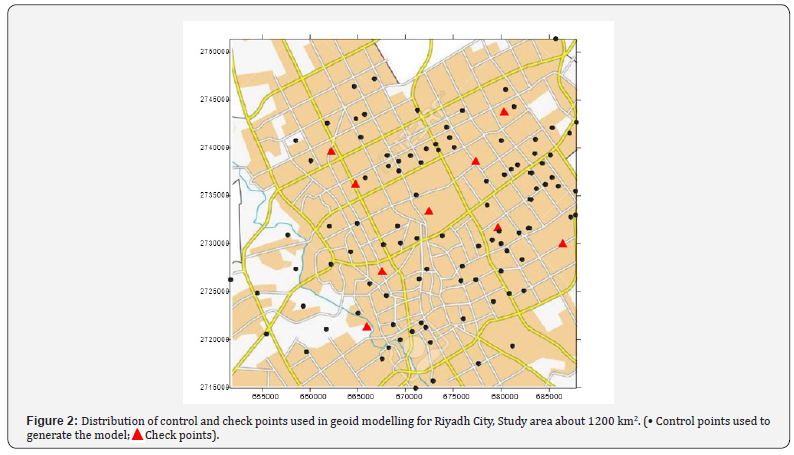
Generally, in big cities, it is possible to find sufficient benchmarks with known orthometric heights. In this paper geometric approach will be adopted to form a geoid model for a limited region: Riyadh city, capital of Saudi Arabia, which extends approximately 35 km x 35 km. 110 control points and 9 check points were available for the geoid modelling process. Figure 2 shows the distribution of these points among Riyadh City. After testing polynomials of different degrees, considering the density of control points to be about one per one square kilometer (110 control points distributed on about 1000 km2) and using multiple regression method, it was found that, the following equation gives the best result:

Using the above equation, the geoidal height N was calculated for all check points (9 points). The difference between calculated and existing value of N for all check point does not exceed 1.8 cm, while RMS error is less than 1 cm. All polynomials of higher degree will improve the accuracy with a very small rate. This result is highly superior to values obtained from EGM 2008 Model for the same points, where the difference exceeds 70 cm. It also competes very well with results of previous studies outlined in the literature review of this paper where best results are between 1 cm and 4 cm.

Conclusion

The accuracy obtained for a geoid model using geometric approach is much better to rely on than the global model EGM 2008. Therefore, it is recommended to apply the geometric method for big cities and for regions that contain enough benchmarks by which the model is generated. The degree of polynomial representing the model, and its parameters, may change from one region to another depending on extend and shape of the region being studied, and, on the number of existing benchmarks. Once an appropriate model for an area is obtained, it can be used directly through configuration process of the receivers before starting the survey works.

For more about Juniper Publishers please click on: https://juniperpublishers.com/journals.php

For more Civil Engineering articles, please click on: Civil Engineering Research Journal

https://juniperpublishers.com/cerj/CERJ.MS.ID.555782.php