Features of Pressure-Free Impregnation of Binders and their Bid in the Practice of Fixing the Moving Desert Sands- Juniper Publishers
Civil Engineering Research Journal- Juniper Publishers
Abstract
Desert sand is subject to deflation. During the construction and operation of railways in the sandy desert, deflation leads to filling the railway track with sand, as well as to soil erosion. To prevent this phenomenon, a binder is sprayed onto the surface of the sand. The penetration of the working composition of the binder into the sand is accompanied by an uneven distribution of the substance, which is proposed to characterize the saturation coefficient. The features of the interaction of the binder and sand from which the protective crust is formed are revealed. Impregnation occurs under the predominant influence of gravitational or capillary forces. The latter allows you to have a uniform distribution of the substance. Preliminary wetting can reduce the pore space of sand and change the nature of the transfer of matter to capillary, which as a result allows obtaining resource-saving technology for fixing movable sand.
Keywords: Capillary and gravitational forces; Concentration; Consolidation; Impregnation; Humidity; Protective crust; Sand deflation; Solvation layer; Specific consumption
Introduction
The transport communications of the world railways and roads are developing steadily. However, due to the need for industrial development, they are built in difficult environmental conditions, for example, in mountains, deserts, in particular in sandy deserts [1-5]. Roads, under these conditions, are adversely affected by climatic events, such as deflation. Deflation causes the roadbed to be blown, and the sand carried as a result of deflation is deposited on the upper structure of the path, saying that the path is entered by sand [6 - 9]. Blowing and drifting are, therefore, manifestations of deflation, its result. These manifestations seriously reduce the traffic safety of vehicles, especially with a steady increase in speed train traffic (Figure 1 & Figure 2). Hence, in the sandy deserts, the study of the negative impact of deflation on the safe construction and operation of communications (roads and railways) and the improvement of the technology to protect them from moving sands is an crucial charge [10-13].


Credentials of encouraging areas of research
There are several methods for fixing moving sands. As a radical measure to achieve a short-term, but immediate result, first of all, they resort to the physicochemical method (PCM) of sand fixation [14, 15]. The essence of FHM is to implement a technological method of spraying a binder on a fixed sand surface with garden sprayers (Figure 3). The liquid without pressure moves into the sandy substrate, permeates it and forms a specific building material - a knitted sand crust, i.e. the binder plays the role of improver of sand, improving its physic mechanical properties, possessing a property that provides stability against the destructive effect of the flow of sand carried by the wind, i.e. wind sand flow [16, 17]. The properties of the crust depend on the properties of its constituents and the features of their interaction, which are manifested in the process of impregnating the sandy substrate with a binder, stabilizing the state of the deflated surface. Owing to these circumstances, it seems important to reveal the features of pressure-free impregnation, to create the theoretical foundations of impregnation and to propose a resource-saving technological solution in the matter of fixing by impregnation of mobile sands.

Basic Terms and Conditions of Non-Preserved Implementation of Sand Substrate by Binding Substances
To date, ideas about the mechanism of sand impregnation with chemical improver do not fully reveal the essence of the phenomenon. Therefore, it becomes necessary to conduct a more detailed theoretical study and summarize the results of previously conducted experiments [16, 18]. For completeness of determining the law of motion of a chemical reliant in sand, the conversion function is not applicable to the vertical impregnation of water into real soils, and the experimental results do not completely coincide with the measured distribution of water in the sol [17, 18]. It is known that impregnation occurs under the influence of gravitational and capillary forces. It is also known that the influence of gravitational forces can be neglected, if and only if the potential energy of the field of capillary forces referred to a unit of liquid is greater than the potential of the field of gravity. According to A.V. Lykov, this is true when the internal size of the channel through which the fluid moves has a size of less than 10–2 mm [19]. Otherwise, the mass of the impregnated liquid cannot be neglected. Therefore, in order to establish the predominant influence on the impregnation process of a particular field of force, it is necessary, first, to determine the internal diameter of the channel formed between the particles of the substrate.
Hydrodynamic approach to solving the problem of impregnating sand with a binder
Imagine fluid transfer as a filtering process. It is fair to assume that the solution to the filtering problem can be approached from the standpoint of the external and internal problems [20] of hydrodynamics, i.e. present as a mixed problem of hydrodynamics [17, 18, 21]. In fact, it can be assumed that the flow moves in irregularly shaped channels formed by the gaps between the particles of the layer (the position of the internal problem of hydrodynamics). On the other hand, it can be assumed that the flow flows around particles of a layer of sand encountered on the way (the position of the external problem of hydrodynamics). Mixed tasks involve the combination of two representations for the purpose of convenience of calculation [22-26]. With a certain degree of idealization, suppose that the main parameters of the problem have the form:
1. specific surface of the particles in a unit volume of the layer Ssk .
2. porosity or fraction of free measurements
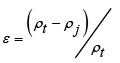
3. grains of sand are a spherical body with an equivalent diameter (de ) .
The experiments will be carried out taking into account the similarity criteria in a vessel with a cross section S, which is filled with sand to a height H and the volume of sand in the vessel v = s. h. . Vessel made of transparent material Initial binder layer.
The experiments (Figure 4) will be carried out considering the similarity criteria in a vessel with a cross section S, which is filled with sand to a height H. The volume of sand in the vessel v = s. h. . Then the surface of the grains can be defined as . s . . s s ss f = v = v h s , and the volume of the solid phase (sand particles) in the vessel according to the formula (1 ) pï V =V −V = S ⋅H ⋅ −ε and the volume of the solid phase (sand particles) in the vessel according to the formula taking into account the similarity criteria, we have: the volume of sand, the surface of the particles, the volume of the solid phase, where p V - is the pore volume
The total resistance of the layer of sand grains is (1)
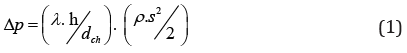
where λ - is the total coefficient of friction resistance and local resistances
Δp - is the total resistance of the granular material
dch - equivalent diameter of polydisperse channels granular material.
From the standpoint of the internal problem of hydrodynamics, the diameter of the channel, as is known, is (2)

where ss s – is the specific surface m2 / m3.
Using the above notation, suppose that the layer contains (n) known difficulties, therefore, in order to overcome. Let particles of an arbitrary shape be in the layer, then the volume of one particle is equal to (3)

The volume of one particle based on its geometric shape can also be expressed as the volume of the ball . d 6 e p v =π . Then the ratio of the surface of the particle to its volume is (4)
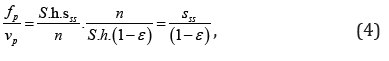
At the same time,
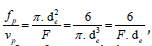

where F - is the shape factor of the particles, given in reference books.
Substituting (2) in (5), we obtain the formula (6)

Taking from the directory F = 0.9; porosity coefficient ε = 0.3–0.45 (the sand porosity of the Kulsary deposit [16], for example, is 44%); the predominant fraction of sand in its granulometric composition d = 0.14 mm, it is possible to obtain an equivalent channel diameter equal to ch d = (3,2-6,86)·10-2 mm > 10-2 mm. those, strictly speaking, the influence of gravity cannot be neglected. This circumstance limits the idealization of the process of impregnation and replacement of real sand with capillary tubes. This means, first of all, that the study of the process of pressure less impregnation of desert sand with a binder should be carried out on physical models. This is all the more true if we take into account that the particle size distribution of the moving desert sands is also represented by the particle size distribution in a rather wide range of particle changes from 0.05 to 0.25 mm (Table 1).
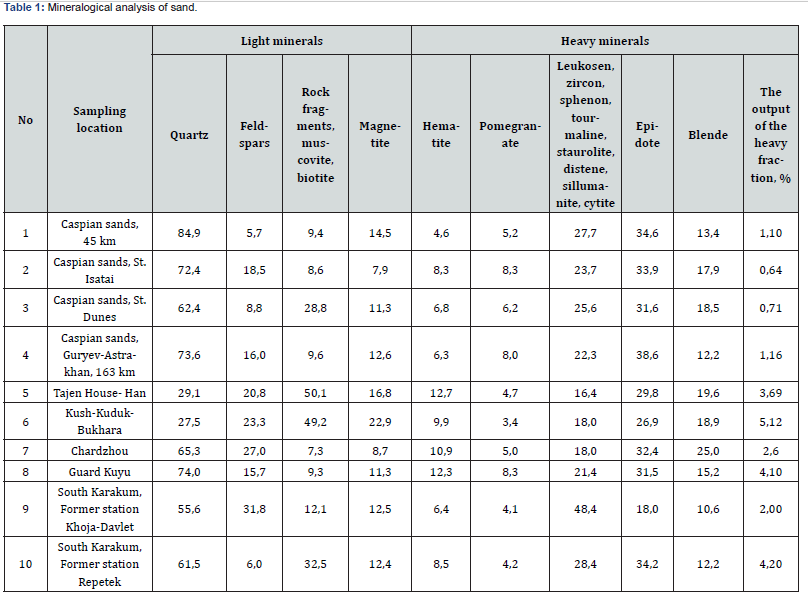
Features of impregnation
From the condition of preservation of the substance (liquid) before and after impregnation, the volume of impregnated liquid (Q) should be equal to the pore volume of the substrate in the impregnated layer (Q1), i.e. Q=Q1. From the condition of maintaining the volume of liquid before and after impregnation, the volume of the impregnated liquid should be equal to the pore volume of the substrate in the impregnated layer 1 2Q = Q .ε where 2 Q – volume of liquid-impregnated sand, ε - bulk porosity, we get. Assuming the area of sand and the area soaked in a chemical ameliorant equal, we get (7)

where δ - is the initial liquid layer above the sand surface, mm.
With free impregnation of sand with multicomponent, non-Newtonian fluids, the impregnation depth will be greater than the theoretically possible value ( ) k h δ > ε . From the point of view of resource saving, excess consumption of chemical reclamant qi > qmax above the maximum is not acceptable.

where n k - is the proportionality parameter, called the coefficient volume of sand saturation with chemical ameliorant. Always with free sand soaking with multi-component, non-Newtonian liquids the depth of impregnation will be more than the theoretically possible value of h δ > ε , close to and more than 1 n k < units indicate that the sand saturation 1 n k ≥ limit has come under these conditions and the initial volume of the chemical ameliorant has not fully soaked. From the point of view of resource saving, excess consumption of chemical reclamant i max q > q above the maximum is not acceptable. From a technological point of view, the excess consumption of chemical improver i max q > q more than the maximum is not acceptable from the point of view of resource saving. Those study of the construction and technological characteristics of the protective layer should be in the range of values of 1 n k ≤ so that i max q ≤ q .
The transfer of emulsions is accompanied by selective wetting of the sand grains with water. A thin film of a liquid is formed, and the dispersed phase of a chemical improver consisting of emulsified particles (according to [15, 22]) is are transferred corky. When impregnated with solutions and multicomponent liquids [16], the pore size narrows during the impregnation process and, as a result, the fluid front movement is unstable due to selective adsorption of the dispersed chemical ameliorant surface particles to the hydration layer, which diffuse from its volume. This phenomenon was confirmed in works [15 - 17]. As a result, this leads to a decrease in the radius of the smallest passages between contiguous particles and a change in the nature of the transfer from the predominantly gravitational to the capillary. Thus, quite unambiguous evidence of the informative value of the saturation coefficient for revealing the nature of the impregnation was obtained. Its values, calculated over the whole range of variation of factors close to unity ( 1) n k < , mean that this binder does not separate when penetrating into the sand, the pore space does not narrow, and the process proceeds under the predominant influence of the field of gravity. If the value of the saturation coefficient is less than unity 1 n k ≤ , and changes in the range of variation of factors n k ≈ 1, then this means that this binder, when penetrating into the sand, separates, and the impregnation process occurs when the pore space narrows under the predominant influence of the capillary field.
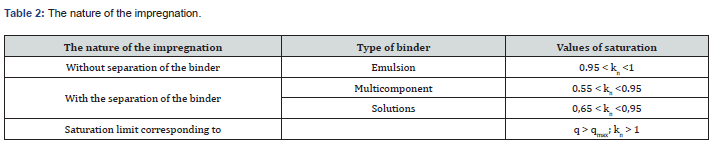
From a technological point of view, these circumstances determine the choice of mode of impregnation and the consumption of a chemical improver. Obviously, for emulsions, the maximum flow rate is determined k_n~1 by the value of the saturation coefficient, whereas for solutions and high-molecular substances ~ 1 n k . In all cases, 1 n k < values close to one indicate that the maximum consumption of the chemical ameliorant is achieved. Excess consumption 1 n k > is not allowed. With this in mind, a classification has been proposed, which makes it possible to identify the maximum level of consumption of a chemical ameliorant in the study of new types of it and to develop on their basis new technologies for fixing moving sands (Table 2).
This circumstance also suggests the idea of using the nature of the character of sand impregnation with binders to increase resource saving and reduce the cost of the method. To d 1 n k > this, reduce the size of the channel formed between the particles of a sandy substrate. For example, soak sand when wet, i.e. in the rainy season or after artificial humidification. The use of locally produced binders in sands of a wet state as a result of reducing the pore space of the substrate will lead to a change in the nature of the impregnation from predominantly gravity to predominantly capillary, which will lead to a decrease in the rate of penetration of the binder into the sand and increase the uniformity of impregnation composition and its specific consumption and, as a result, obtaining a number of alternative resource-saving technological solutions Repetitions of mobile sands by a physicochemical method.
Choice criteria for evaluating the strength of protective layer
From the analysis of literature and regulatory sources, the requirements for anti-deflation protective coatings were established: fast elastic deformation modulus E1 <8x106 Pa, slow elastic deformation modulus E2 <1,1x106 Pa, equilibrium elastic modulus E <4,4x106 Pa, the highest plastic viscosity η > 1,05x106 Pa s [14]. In some studies, it is noted that the main criteria for evaluating the optimal structure of the protective layer can also be shear deformations: elasticity λ , static plasticity, and the period of true plastic relaxation [17]. Thus, the state of the protective crust is evaluated by many indicators. Only to clarify the possibility of implementing the main technological method of the physicochemical method of fixing sand - impregnation of a binder and obtaining a stable protective crust, it is necessary to conduct a sufficiently large amount of experimental research. In addition, the whole variety of physico-mechanical characteristics and parameters can be expressed in a generalized form by plastic strength m P > 3x103 Pa [18]. Given these circumstances, the study was proposed to be carried out in two stages: at the first stage, the possibility of using one or another binder with respect to the degree of impregnation and plastic strength is assessed, then, with a positive result, at the second stage, an in-depth study of the properties of the protective peel. These studies should be considered as a theoretical understanding of the performed experimental studies and the results of experimental studies published in the journal СERJ in 2019 [27].
Conclusion
1. Deflation is an exogenous process that negatively affects the state of the railway. Deflation can be stopped in various ways. The most technologically advanced is the physicochemical method of fixing moving sand using various binders. When sprayed, binders penetrate the sand and impregnate it.
2. When forming the structure of the protective peel, impregnation is important. Impregnation can be considered as the movement of a substance without pressure in the porous body of a sandy substrate. Then the impregnation process can be represented as a hydrodynamic problem.
3. When a joint consideration of the external and internal problems of hydrodynamics, taking into account the distribution of particles, it is possible to obtain the equivalent diameter of the pore space for real moving sands. As a result, it was found that the impregnation occurs under the predominant influence of gravitational forces.
4. Ensure uniformity of impregnation and more complete saturation of the pore space with binders, it is necessary that the impregnation occurs under the predominant influence of capillary forces.
5. Realize the capillary nature of the binder impregnation, it is proposed to moisten the sand in a natural or artificial way. Then the solvate layer of moisture increases with a decrease in the pore space of sand. At the same time, the concentration of the substance in the working composition and its specific consumption also decrease, which opens up the prospect of creating a number of alternative resource-saving technological solutions for the fixation of moving sands by the physicochemical method.
6. It was found that the sand moisture factor is a source of reducing the binder consumption by 10-15% and increasing the period of the year suitable for fixing movable sand. Thus, wet sand impregnation allows improving the technology and achieving resource savings.
For more about Juniper Publishers please click on: https://juniperpublishers.com/journals.php
For more Civil Engineering articles, please click on: Civil Engineering Research Journal
https://juniperpublishers.com/cerj/CERJ.MS.ID.555787.php


Comments
Post a Comment