Study of Structure Oscillations Under One-component Kinematic Effect-Juniper Publishers

Civil Engineering Research Journal

Abstract

Mathematical statement, methods and algorithm to solve the problem of steady-state forced vibrations of a structure are given in the paper using spatial model with account of viscoelastic properties of material of various structures and their elements under one-component kinematic effect. The results of study of earth structure oscillations under one-component kinematic effect are presented.

It is stated that:

A. for the structures under consideration in dynamic calculations it is desirable to use a spatial model;

B. viscoelastic properties of soil under the load effect slightly reduce the amplitude of oscillations, and after effect cessation these properties lead to a sharp attenuation of structure oscillations.

Keywords: Earth structure; One-component effect; Dynamic calculation; Resonance; Attenuation; Viscoelastic properties of soil; Plane and spatial models

Introduction

Studies have shown that for reliable investigation of structure and equipment oscillations, the possibility to use plane or spatial model depends mainly on the geometric parameters and inhomogeneous features of these objects and the nature of their strain under possible combinations of different loads. For example, when calculating various structures, only one component of seismic effect is taken into account in current regulatory documents on earthquake engineering. It is believed that the vertical acceleration is less than the horizontal one. However, engineering analysis of the aftermath of various earthquakes has shown the presence of some damage, the nature of which is difficult to explain by the action of horizontal component of seismic effect [1-3].

According to seism metricsss observations, it has been stated that at strong ground motion, along with the horizontal component of acceleration, other components of accelerations predominate [4-6]. To reliably assess the strength of a structure, it is necessary to answer the questions - when it is necessary to use plane or spatial model of structure and which components of the earthquake’s accelerogram should be used as external effects.

In recent studies of structure oscillations, the use of a plane model of structure under one-component effect is mainly considered, and in rare cases two-component kinematic effect [7-16].

Therefore, in this paper an attempt is made to investigate the oscillations of various earth dams using the spatial model of a structure, taking into account viscoelastic properties of soil and the inhomogeneous features of a structure under one-component acceleration of an earthquake. To answer these questions when studying structure oscillations, it is necessary to consider the problem of determining the components of the displacement vector and the stress tensor with time arising at the points of the structure at different directions of non-stationary dynamic effects using a spatial model.

Materials and Methods

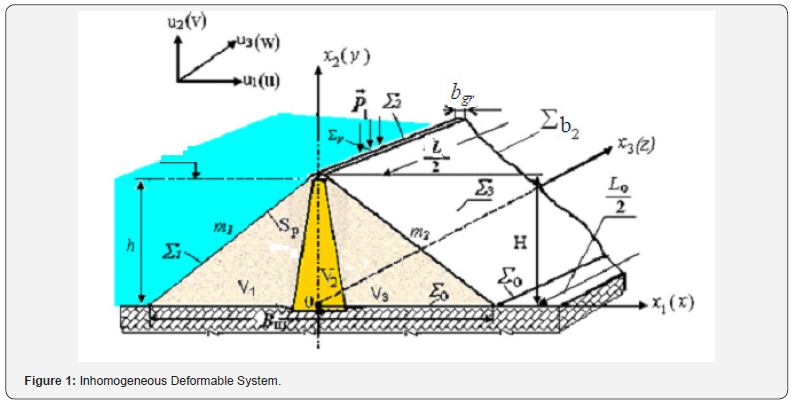
An inhomogeneous system is considered (Figure 1) in the paper; it consists of deformable bodies of volume V = V1+V2+V3. The lower part of the system is located on a rigid base S0, where a kinematic effect 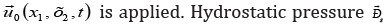(x1,х2) acts on Sp part of the surface S1 , and the remaining part (S2, S3) of the surface is stress free. The system (Figure 1) is a massive body, so the calculation takes into account mass forcesf. Material of different parts of the system is considered linearly elastic or viscoelastic. At the boundaries of the system regions (Figure 1) the displacements, the stress components are continuous.

The task is to determine the displacement and stress fields of the system (Figure 1), taking into account mass forcesf, water To state the problem, the principle of virtual displacements is used, according to which the sum of work of all active forces, including inertia forces, on virtual displacements is zero [17]:

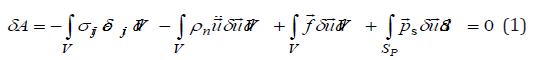
Here u, εij , σij are the displacement vector and the components of the strain and stress tensors, respectively; δu , δεij are isochronous variations of displacements and strains; n ρ is the density of material of the system elements; f is the mass force vector; s p  is hydrostatic pressure of water. Hereinafter, the index n=1,2,3 means the element of the system (i.e. the volume V) the given mechanical characteristics refer to.

To describe the properties of viscoelastic material of the elements of the system (Figure 1), the heredity Boltzmann- Volterra theory [18] is used, according to which the relations between the stress σij and strain εij tensors have the form [18,19]:

To simulate the dynamic process in the system (Figure 1), kinematic conditions at the base are also set.

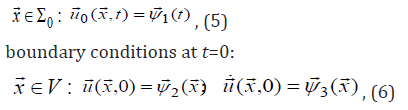
where is the given function of time; 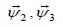, are the given functions of coordinates. Displacement vector has three components . Variation problem considered above using the procedure [20] of the finite elements method (with spatial finite elements) is reduced to a resolving system of integro-differential equations of large order, that is:

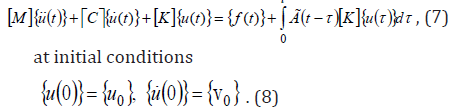
Here, [M], [K] are the matrices of mass and stiffness of the entire structure; [C] is the matrix of dissipative forces, if internal friction is taken into account in structure material; {u(t)} is the vector of sought for displacement amplitudes; {f (t)} is the vector of external load from kinematic effect and hydrostatic pressure. In assessment of the dynamics of considered dams, the order of solved systems of integro-differential equations reached 1700. Systems of integro-differential equations (7) with initial conditions (8) are solved by the Newmark method [20]. Using the procedure of the Newmark method, the system of integrodifferential equations (7) can be reduced to an algebraic system of equations

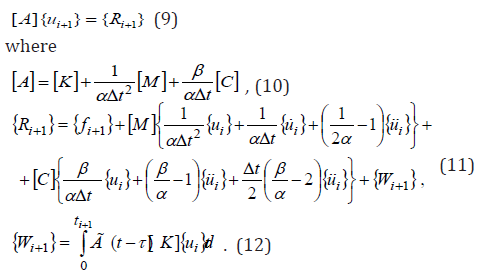
The Newmark method is unconditionally stable if the coefficients of remainder terms are

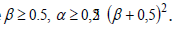.Thus, the solution of integro-differential equations (7) with initial conditions (8) is as follows:

A. Initial values are set:

B. A system of algebraic equations (9) and (10) is formed, the right-hand side (11), (12) contains the terms describing viscous properties of material, depending on strained state of the system.

C. The resulting system of algebraic equations is solved by the Gauss method or the square root method.

A feature of the algorithm is that the integrals entering the expression (12) of the vector {Wi+1} are calculated from the beginning of the process, while at each step the integrals are calculated in the range from ti to ti+1. In this case, the total value {Wi+1} at time ti+1 is obtained by summing the value {Wi} saved at the previous step and the integral obtained at the last stage with the integration limits from ti to ti+1.

In concrete calculations, the Rzhanitsyn kernel [21] is used to describe viscoelastic properties of soil; viscoelastic parameters of soil are given in [22].

Results

The dynamics of the model of the Gissarak earth dam under the effect of various loads is investigated in this paper.

The Gissarak dam [17] has: geometrical dimensions - (H=138.5m, bgr=10.0m, 2.2, m1 =2.2 m2 =1.9 ); physical-mechanical characteristics of material of various sections are (for the dam core: G=2780 kgf/sm2, ν=0.37, γ=0.0017 kgf/sm3; for the transition zone: G=3500 kgf/sm2, ν=0.35, γ=0.00215 kgf/sm3; for retaining prisms: G=3210 kgf/sm2, ν=0.30, γ=0.0019 kgf/sm3; for slopes strengthening: G=8400 kgf/sm2, ν=0.25, γ=0.0024 kgf/sm3).

Here H is the height of the dam; bgr is the width of the crest; m1, m2 are the coefficients of the rate of upstream and downstream slopes; γ is the specific weight of material; ν is the Poisson’s ratio; G is the shear modulus of elasticity.

For a further study of structure dynamics, the kinematic effect at the base of the structure S0 has the form

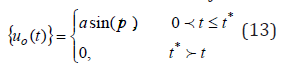
Here: p - is the frequency; a - is the amplitude; t* - is the time of the effect; t - is the time of the process studied.

The displacements of various points of the dam in time have been determined under each effect using a spatial model. The parameters of the kinematic effect are taken as: a=0.01m, t*=5 seconds; p=5.70 rad/sec.

Figures 2-4 show the time variations of displacements of the point (x1=8m, x2=138.5m, x3=330m) on the crest of the Gissarak dam, obtained with spatial model under one-component kinematic effects (different in directions) in the pre-resonant mode of oscillation. The solid line in Figure 2-4 corresponds to elastic solution, the dotted line is obtained taking into account viscoelastic properties of soil. Analysis of the results obtained shows that under one-component effect the displacements of the point in direction of the effect exceeds the displacements of the point in other directions by an order of magnitude (Figures 2-4). That is, one-component effect causes displacements of the model point, basically, only in the direction collinear with the effect; the remaining displacements (in orthogonal direction) are insignificant (Figure 2).

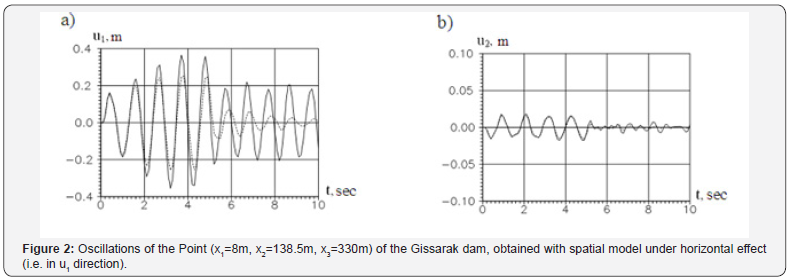
Therefore, under horizontal effect (i.e. perpendicular to the longitudinal axis of the dam) the use of plane model in the assessment of dynamic behavior of a dam is justified, since in this case the components of the tensor of displacement in longitudinal direction to the dam plane, i.e. u3 is less by an order of magnitude than u1 and u2.

Under vertical effect the tensor components of the displacements in transverse (horizontal) direction u1 are by an order of magnitude less than u2 and u3, which are also orthogonal to the direction of the effect. Under such effect, it is advisable to use a spatial model, which allows to determine vertical displacements of points not only of the central cross section (as in plane model), but also vertical displacements of points of dam site.

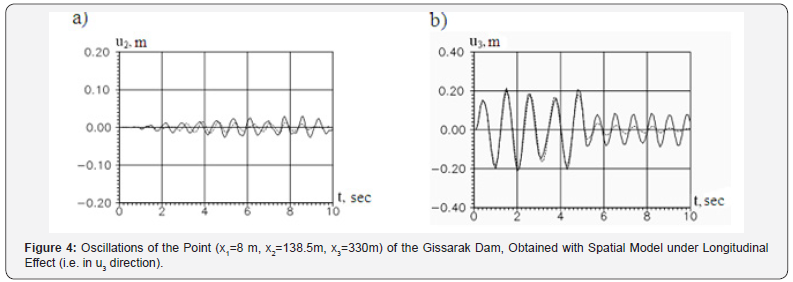
Under longitudinal effect the tensor components of the displacements in transverse (horizontal) and vertical directions, i.e. u1 and u2 are by an order of magnitude less than u3 in longitudi nal direction. For the same reason, the spatial model can also be used when calculating a structure under longitudinal kinematic effect, which causes mainly longitudinal displacements of points (Figure 4). Analysis of the results obtained shows that viscoelastic properties of soil under load effect slightly reduce the amplitude of oscillations of the structure, and after effect cessation these properties lead to a sharp attenuation of oscillations. When taking into account elastic properties of soil after effect cessation, the oscillations do not attenuate, and the structure oscillates with the amplitude reached at the time of effect cessation at fundamental natural mode of oscillations (Figure 2-4).

Conclusion

A. Methods and algorithms to study the dynamics of earth dams using a spatial model and taking into account viscoelastic properties of soil under one-component kinematic effect are presented.

B. Analysis of dynamic behavior of the dam under consideration has shown that for a given dam under horizontal effect it is possible to use a plane computational model, but under other effects it is necessary to use a spatial model of a structure.

C. Viscoelastic properties of soil under the load lead to a slight decrease in the amplitude of oscillations, and after effect cessation, to a sharp attenuation of structure oscillations.

References

For more open access journal, please click on Juniper Publishers

For more civil engineering articles, please click on Civil Engineering Research Journal

https://juniperpublishers.com/cerj/CERJ.MS.ID.555698.php

Search This Blog

Juniper Publishers Journal Of Civil Engineering