Optimal Pump Scheduling Considering Resetting Reservoir to Minimum Level and Rescheduling due to Pump Maintenance- Juniper Publishers
Juniper Publishers- Journal of Civil Engineering
Abstract
In this paper we consider two pumping stations, one
with three pumps that can be run individually or as combinations and the
other with one pump as well as daily maximum volume restriction on
water to be pumped out. Night electricity tariffs are lower than day
tariffs. Each hour has its constant demand except the 7th hour where demand varies, 7th
hour demand variation notice is sent a day before by the water
customer. Water from these pumping stations is pumped to a high point
service reservoir so that pressure level can be maintained on taps.
Service reservoir has a capacity of 10000m3 and the water level should
not go below 40% full in order to safeguard supplies in the event of
burst water and to meet sudden demands such as firefighting. Linear
programming is used to determine which pump combination is to be used
during which hour as well as developing optimal schedules when any pump
is under maintenance
Keywords: Scheduling; Linear programming; Water pumps; Pump maintenance
Abbreviations: IP: Integer Programming; MOEA: Multi-objective Evolutionary Algorithms
Introduction
Significant percentage of energy consumption in the
world is used for pumping purposes as a result there is need for pump
scheduling with objective of minimizing electricity consumption. Ordan
et al. [1]
developed a new methodology for optimized real-time operation of a
water distribution. The methodology is based on the integration of three
models, namely the real-time demand forecasting model, the hydraulic
simulation model, and the optimization model. The optimization process
is driven by the cost minimization of the energy used for pumping and
the maximization of operational reliability. Optimal pump schedules were
generated by using a multi-algorithm-genetically-adaptive- method
(AMALGAM), they also performed hydraulic simulations using the EPANET2
model. Lansey and Awumah [2]
presented a methodology for determining optimal pump operation
schedules for water-distribution systems. In addition to minimizing the
energy-consumption cost, their model includes a constraint to limit the
number of pumps that are switched on during the planning period. They
also adopted a two-level approach whereby the system hydraulics are
analyzed in an off-line mode to generate simplified hydraulic and cost
functions for an on-line model. These functions developed for each pump
combination allow for rapid evaluation within a dynamic programming
optimization algorithm.
Racca et al. [3]
presented a new optimal pumping scheduling model that integrates the
evaporation losses from the reservoirs into the optimization algorithm
and provides the optimal pumping policy that minimizes both pumping and
water costs. Multi-objective Evolutionary Algorithms (MOEAs) were
considered to solve an optimal pump-scheduling problem with four
objectives to be minimized, thus electric energy cost, maintenance cost,
maximum power peak, and level variation in a reservoir [4]. Wang et al. [5] enhanced genetic algorithm for bi-objective pump scheduling in water supply. Hyeong-Seok et al. [6]
applied a binary integer program to optimize pumping schedule of a
water supply system in Polonnaruwa, Sri Lanka based on the hourly water
demands for the next day. The water demands were forecasted by a
combined model consisting of an autoregressive integrated moving average
model and an error compensation routine based on exponential smoothing
technique. The result showed that the optimization system could reduce
the operation cost of the WSS by minimizing electricity for
water-pumping; electricity cost for pump operation could be reduced by
55%. For the past decades, a few forecasting methods have been applied
to optimize pumping schedules of WSSs [7]. Genetic algorithm also has been applied for minimization of pumping cost through intermittent water pumping in a WSS [8].
Giacomello et al. considered a hybrid optimization method for effective
pump scheduling. They solved the problem by a novel hybrid optimization
method that uses linear programing and a greedy algorithm. Naoum-Sawaga
et al. [9]
proposed new approaches for water pump scheduling and pipe replacement,
they also applied a knapsack based heuristic for the leak pipe
replacement problem. Jowitt and Germanopolous [10]
considered a method based on linear programming for determining optimal
schedule of pumping on a 24 hour basis. They considered both unit and
maximum demand charge, as well as efficiencies of the available pumps,
the structure of the electricity tariff, the customer demand profile,
and the hydraulic characteristics and optimization constraints of the
network. Sakarya and Mays [11]
determined optimal operation of water distribution system pumps with
quality considerations. Integer programming (IP) was also applied by Kim
et al. [12], Biaszczyk et al. [13]
presented the optimal pump scheduling for a large scale water
distribution system by applying linear programming to optimize the
operating schedule of the pumping system in the Seoul Metropolitan area.
They used a multiple regression model to forecast hourly water demands.
Bagirov et al. [14]
introduced a novel approach for modelling of explicit pump scheduling
to minimize energy consumptions by pumps which uses the pump Start/ End
run times or continuous variable, and binary integer variables to
describe the pump status at the beginning of the scheduling period.
Pasha and Lansey [15]
linearized pump stations relationships using relationships among energy
required, pumping flow, demand factors, tank storage or tank water
levels. They formulated a linear programming model and solved for a
single tank system for the optimal pump schedule to minimize energy
costs. Bragalli et al. [16]
proposed a method to design optimal distribution reservoirs and their
operation using non-linear programming. Price and Ostfeld [17]
examined problem that includes nonlinear convex headloss, leakages and
varying total head pump energy consumption constraints. Savic et al. [18]
introduces multi-objective Genetic Algorithms (GAs) for pump scheduling
in water supply systems. The two objectives considered were
minimization of energy and maintenance costs. Pump switching were
introduced as a surrogate measure of maintenance cost. The
multi-objective algorithm was compared to the single objective GA, with
both techniques improved by using hybridization with a local-search
method.
Statement of the Problem
Distribution of potable water requires that water is
pumped to reservoir at high point in the system. Pumping uses
electricity which has a cost which varies through the day. Considerable
saving in electricity costs can be made by choosing when pumping is done
but pumping patterns are constrained by the necessity to safeguard
supplies. In this case study water is obtained from three different
types of source
1. Surface reservoirs,
2. Underground, and
3. Abstraction from rivers.
Water is treated in various ways to make it both safe
and acceptable to drink. The treated water is pumped to the reservoir.
The service reservoir is situated at high points of the distribution
system so that the water pressure is maintained at the taps. Since the
service reservoir is at high points of the system it is necessary to
pump treated water to this reservoir. Often there are several pumps at
the pumping station which are situated at the water treatment works.
Various combinations of pumps can be used at the request of the
operator. Pumps can be controlled either by switching them on or off.
The water companies spend a lot of dollars per annum on electricity of
pumping water. Table 1
gives electricity tariff which clearly shows that pumping is cheaper at
night than during the day. The flow of water down a pipe is subject to
some frictional force from the walls of the pipe which increases at the
rate of flow of water increases. Table 2 & 3
gives the power consumption and flow rates for all possible
combinations of pumps at Nyamandlovu and Sgodini pumping stations which
supplies the Bulawayo reservoir. The Esigodini treatment works can only
treat 2000 cubic meters of water per day. The hourly demand for water
for the Bulawayo community is given in Table 4.
The Bulawayo service reservoir has a capacity of 10000 cubic meters and
the water level should not go below 40% full in order to safeguard
supplies in the event of burst water and to meet sudden demands such as
for firefighting. A pump schedule is a set of instructions to the
operator as to when the pumps at a pump station must be switched on and
off. A pump schedule is needed that satisfies demand at the minimum
costs while satisfying constraints of the water level in the Bulawayo
service reservoir. Pump reschedule is also necessary when a certain pump
is under maintenance so as to optimally pump water with the available
pumps.



A unit cost for every kilowatt hour energy that is used is given in the Table 1.
Sgodini Station has 1 pump (Table 2).
Nyamandlovu Station has three pumps, two of type A and one of type B pump which may be run in any combination given in Table 3 below.
Linear Programming
Linear programming model is modelled in such a way
that the solution output indicates minutes in a given hour a pump or
pump combination is supposed to be switched on and off during the day
and night. The model output is such in a way that it can be used to draw
up pump schedules as well as determining the utilization of pumps.
Linear programming model parameters
τ0 —— Hourly cost for using pump (A) during the night
τ1 Hourly cost for using pump (A) during the day
ϵ0 Hourly cost for using pump (B) during the night
ϵ1 Hourly cost for using pump (B) during the day
γ0 Hourly cost for using pump combination (A+B) during the night
γ1 Hourly cost for using pump combination (A+B) during the day
δ0Hourly cost for using pump combination (A+A) during the night
δ1Hourly cost for using pump combination (A+A) during the day
μ0Hourly cost for using pump combination (A+A+B) during the night
μ1Hourly cost for using pump combination (A+A+B) during the day
ρ0Hourly cost for using pump (SGODINI) during the night
ρ1Hourly cost for using pump (SGODINI) during the day
D;KDemand during hour K
Θ Output flow rate of pump j in cubic metres per hour, and j
= Pumps (A,B, A+B, A+A, A+A+B, SGODINI)
p (j) NNK → Pump j at Nyamandlovu, during the Night, during hour K, and j
=Pumps (A,B,A+B,A+A,A+A+B,)
p (j) NDK → Pump j at Nyamandlovu, during the Day, during hour K, and j
=Pumps (A,B,A+B,A+A,A+A+B,)
p (j) SNK → Pump j at Sgodini, during the Night, during hour K, and j=SGODINI pump
p (j) SDK → Pump j at Sgodini, during the Day, during hour K, and j=SGODINI pump
μ Reservoir capacity
® S — SGODINI pumping station capacity
℧ K — Water accumulated at hour K
Linear programming model
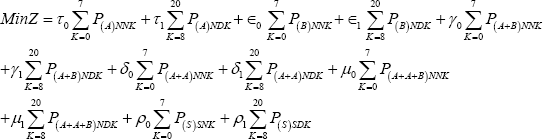
Constraint set number 1
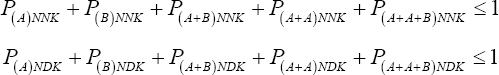
Constraint set number 2
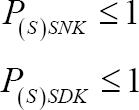
Constraint set number 3
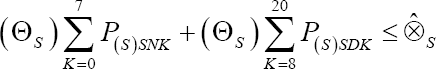
Constraint set number 4
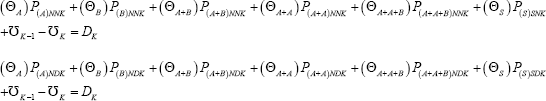
Constraint set number 5
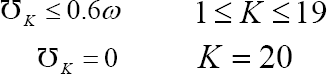
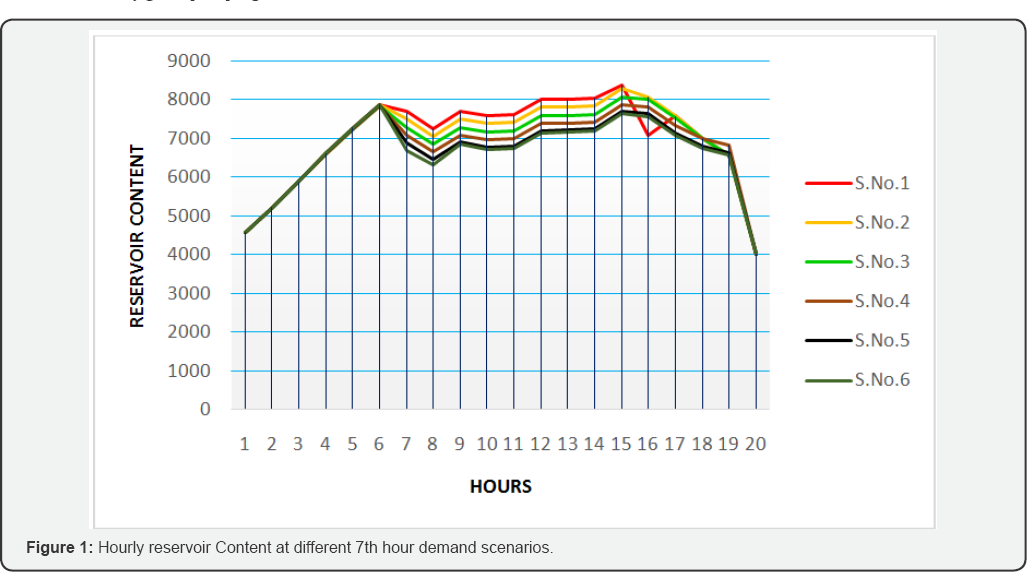
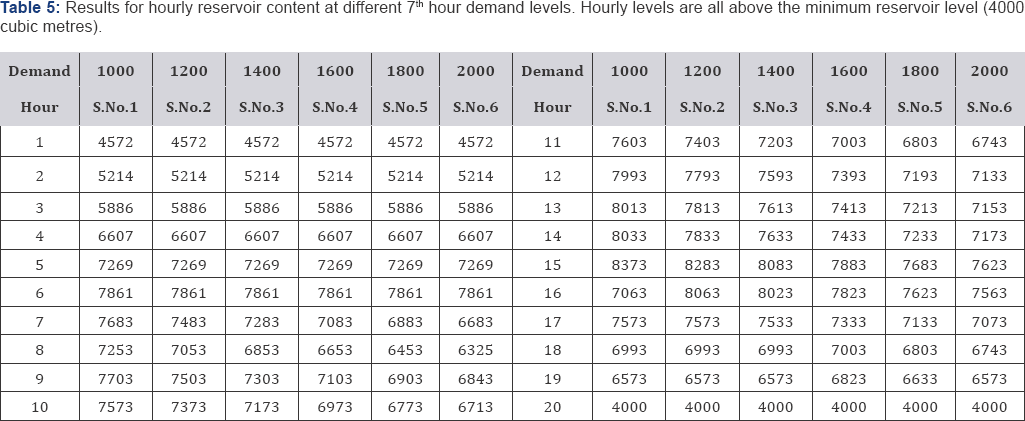
Results (Table 5 & 6, Figure 1 & 2)
Table 6
shows how many minutes a pump is supposed to be switched on in any
given pumping hour. It is from this table where pump utilization
information is taken from. Optimal scheduling cost at different 7th
hour demand scenarios are as follows: 1000 cubic meters ($110.16), 1200
cubic meters ($113.36), 1400 cubic meters ($116.56), and 1600 cubic
meters ($119.76), 1800 cubic meters ($122.96), and 2000 cubic meters
($126.84).
Utilization of Pump A decreases as demand level
increases, this indicates that Pump A is not economic and optimal to use
for long time when demand level is high. Sgodini pump utilization level
is uniform even if demand is increasing. Pump combination (A+A) and
(A+A+B) increases utilization level as demand increases, this is so
because these pump combinations are able to pump high volumes of water
to satisfy increasing demand levels as well as minimum reservoir
content.

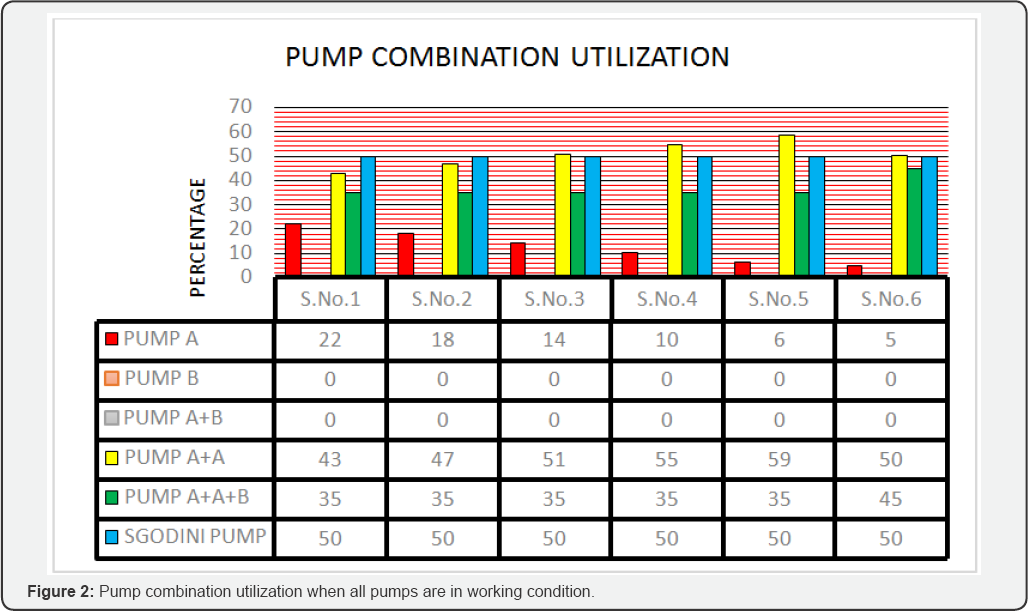
Pump Rescheduling
We assume that at most one pump is under maintenance
in any given day. The unavailability of any given pump due to
maintenance doesn't only affect the total number of pumps available, but
it also reduce the total number of pump combinations to be used. In
this case we want to make use of available pump combinations to
optimally pump water to Bulawayo reservoir. On the other hand we should
bear in mind that we are only supposed to pump water to our customer if
and only if we can satisfy the 7th hour demand, thus not violating minimum reservoir level restrictions in the pumping long run.
Assuming that pump B is under maintenance
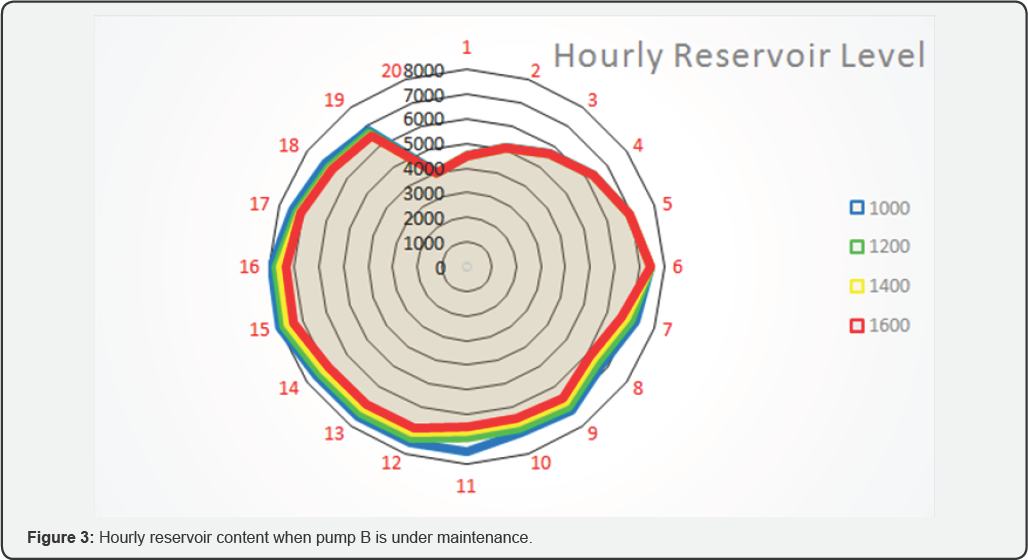
When pump B is under maintenance, we remain with
three pumps to be scheduled, thus pump A, A+A, and Sgodini pump. These
pumps when scheduled using linear programming the solution lies within
the infeasible region when demand is above 1600 cubic meters (Table 7, Figure 3).
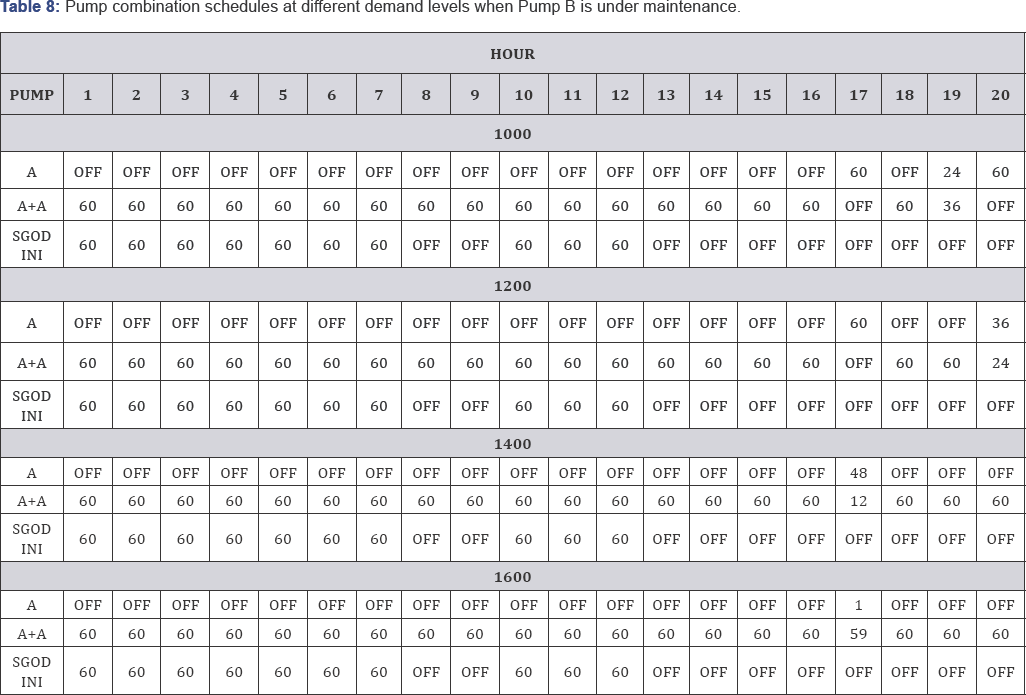
When pump B is under repair, we have three pump
combinations to be scheduled thus, Pump A, Pump A+A, and Sgodini pump.
These pumps were scheduled in such a way that minimum reservoir content
was not violated as well as When Pump B is under repair or maintenance
these pumps combinations can only pump a maximum 7th hour
demand of 1600 cubic metres. In general when pump B is not working we
cannot supply a demand above 1600 when using available pumps. Optimal
scheduling cost at different 7th hour demand scenarios are as follows:
1000 cubic meters ($114.65), 1200 cubic meters ($117.85), 1400 cubic
meters ($121.76), and 1600 cubic meters ($128.56) (Table 8, Figure 4).
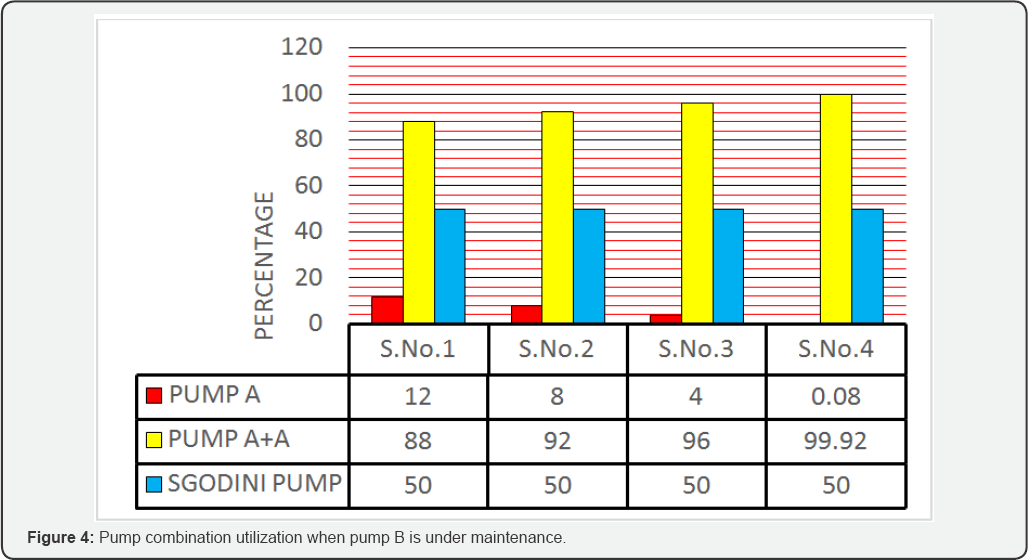
Pump (A+A) utilization factor as demand level
increases. When demand level is at 1600 cubic metres pump (A+A) has to
work almost throughout the day, with 99.92% utilization, and pump A is
utilized for 0.08%, and this implies that pump A is not capable, optimal
or economic when demand level increases. Utilization of Sgodini pump is
uniform throughout deferent demand levels (50%).
Assuming that sgodini pump is under maintenance
When Sgodini pump is under maintenance, pumps A, B,
A+A, A+B, A+A+B are the ones available for rescheduling. The optimal
schedule of these pumps cannot supply demand capacity above 1000 cubic
meters. The optimal cost for pumping when 7th hour demand is 1000 cubic meters is $144.75 (Table 9 & 10, Figure 5 & 6).
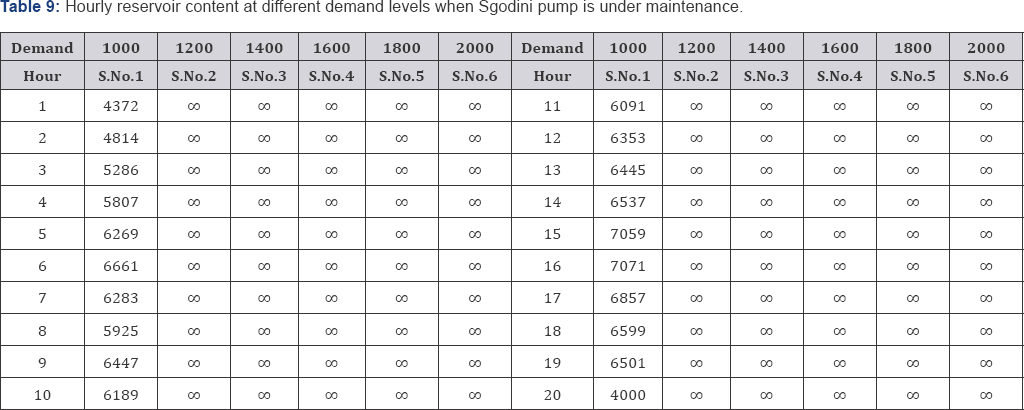
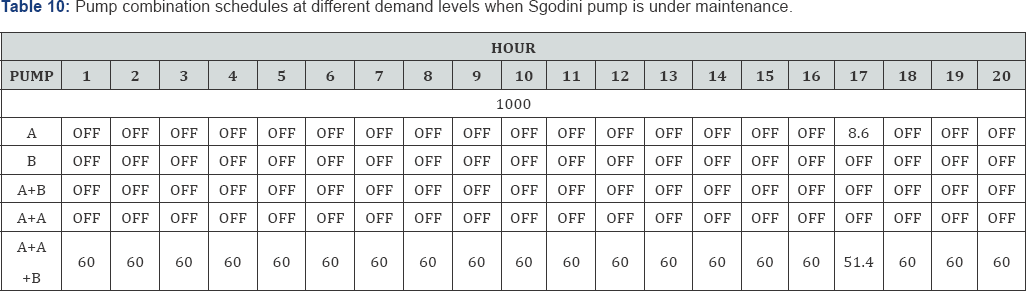
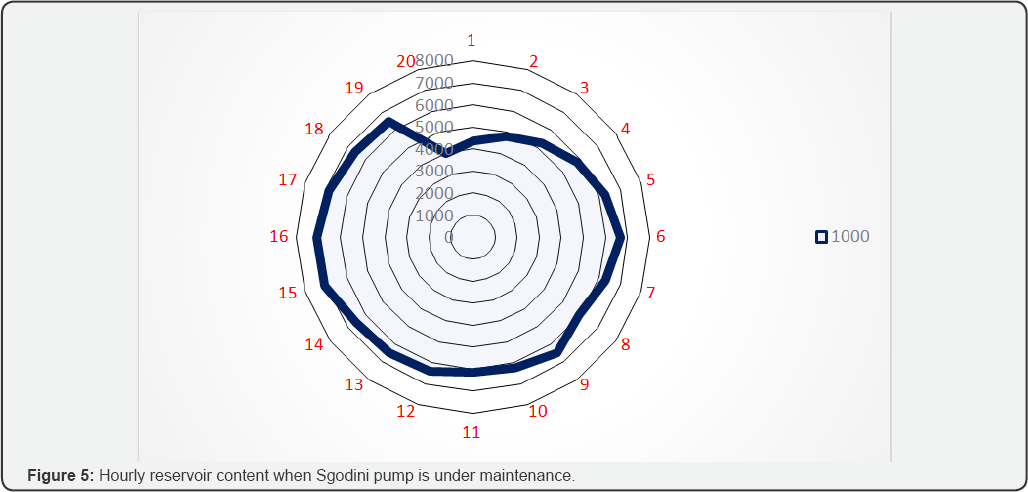

When Sgodini pump is under maintenance we can only
supply a minimum and a maximum of 1000 cubic metres. The utilization of
pumps are as follows, Pump A (%0.663), Pump B (%0), Pump A+B (%0), Pump
A+A (%0) and Pump A+A+B (%99.28). This indicates that Sgodini pump in
important pump type when supplying levels of demand more than 1000 cubic
metres. On the other hand this reveals that Pump B, Pump A+B, and Pump
A+B are dependent of Sgodini pump. When Sgodini pump is under
maintenance, any demand level more than 1000 cubic meters lies within
the infeasible region.
Assuming that pump A is under maintenance
When pump A is under maintenance, pumps B and Sgodini
are the only ones available for rescheduling. The solution for
scheduling these pumps lies in the infeasible region. This implies that
they are not capable of supplying the 7th hour demand levels.
Conclusion
We have significantly demonstrated how linear
programming can be used to optimize pumping costs as well as scheduling
1600 pump combinations. Since we can supply a maximum of cubic meters
when pump B is under maintenance, a maximum cubic metres when Sgodini
pump is under maintenance, 100 of and a maximum of zero cubic meteres
when pump A is under maintenance, this indicates that pump A is very
useful to meet cubic meters and more. Pump B is useful 1000 demand
levels of cubic metres, 1600 to supply demand level which is more than
pump Sgodini is useful for supplying demand level which is more cubic
metres. In general if the pumping company needs 1000 than to invest in
buying new pumps it has to buy pumps of type A and Sgodini pump type.
Furthermore, the results have shown that Pumps (B, A+B, A+A) are not
economic or capable when Sgodini pump is under repair, this is evidenced
by their utilization of .zero percent when Sgodini pump is under
maintenance
For More Open Access Journals Please Click on: Juniper Publishers
Fore More Articles Please Visit: Civil Engineering Research Journal


Comments
Post a Comment