Finite Element Analysis and Theoretical Study of Punching Shear Strength of Concrete Bridge Decks- Juniper Publishers

Juniper Publishers- journal of Civil Engineering

Abstract

The problem of punching shear usually arises in reinforced concrete slabs subjected to concentrated loads and particularly in concrete

bridge decks due to the development of an internal arching system. Ongoing research revealed that the governing mode of failure for concrete bridge decks is not flexure and that using the flexural design method usually led to unnecessary high levels of steel reinforcement. This paper examines the applicability of the non-linear finite element formulation of restrained concrete bridge decks. A special purpose finite element program FEMPUNCH was developed and employed in this study along with the commercially available finite element programs. The accuracy of non-linear finite element analysis is demonstrated using test results conducted by other researchers. The results of the finite element analysis are also compared to those obtained from a non-linear mechanics model developed by Mufti and New hook. The experimental results and the theoretical model provide insight to the fundamental behaviour of concrete bridge decks.

Keywords:Polypropylene; FEMPUNCH; Bridge deck slabs

Abbrevations:GFRP: Glass Fibre Reinforced Polymer; PFRC: Polypropylene Fibre Reinforced Concrete; CHBDC: Canadian Highway Bridge Design Code; ANACAP: Anatech Concrete Analysis Program

Introduction

Concrete slab-on-girder bridge decks have been a popular choice for many short and medium span bridge applications throughout North America. The authors of this paper have been part of a Canadian research team, which has been empirically and theoretically studying the behaviour of these decks for several decades [1,2]. Of principal interest is the strength of these decks under concentrated wheel loads. This on-going research effort has improved our understanding of the key mechanisms associated with the strength and stiffness of these decks and the importance of in-plane restraint in the performance of concrete bridge deck slabs. Innovative bridge deck designs have been developed [3] and applied to several highway bridges and other structures in Canada [4] and more recently in the United States.

This paper reports on the theoretical study of the punching shear behaviour in restrained concrete bridge deck slabs of girder bridges with emphasis on the analytical comparison of non-linear finite element analysis and the PUNCH program developed by Mufti & Newhook [1]. While the design practice is generally to estimate punching shear strength in concrete using simple empirical equations, these equations provide little guidance as to the mechanisms involved and the impact of various parameters on design. The work summarized in this paper helps identify for the design engineer, the basic behaviour of the system, the conditions which lead to punching failure and to demonstrate how non-linear finite element analysis can be adopted to predict the behaviour of these systems, not just to estimate ultimate load. The accuracy of the non-linear finite element analysis was demonstrated using test results available in the literature. The results of the finite element analysis have also been compared to those obtained from a mechanics model developed by the authors.

Externally Restrained (Steel-Free) Concrete Bridge Deck Concept An externally

An externally restrained steel-free concrete bridge deck slab [2] consists of providing a system of steel straps between adjacent girders to restrain any lateral movement of these girders. All internal reinforcement can be removed; internal glass fibre reinforced polymer (GFRP) crack control reinforcement may be added if desired [3]. Research has also shown that the bottom transverse reinforcing bars act as ties for this same arching action mechanism rather than as flexural reinforcement for the perceived moments [5]. Deck slabs with internal reinforcement of either steel or FRP [3] are therefore considered to be internally restrained deck slabs. Under concentrated wheel loads, the restraining elements develop increasing tensile stresses and provide a lateral restraining force to the concrete deck slab. As a result, compressive membrane forces within the deck slab are developed. The degree of lateral restraint provided will determine the ultimate load at which the deck fails in punching under concentrated loads such as vehicle wheel loads.

Response of concrete deck slabs to wheel loads

Extensive field and laboratory testing on concrete deck slabs subjected to wheel loads indicates that two structural responses occur. The initial response is primarily flexure, which leads to the formation of longitudinal cracks on the underside of the deck between adjacent girders. After the formation of the first longitudinal crack, however, compressive membrane action or arching also forms a component of the response mechanism. If sufficient lateral restraint exists, then the arching response will dominate the latter stages of the loading behaviour and failure will occur through punching of the deck slab.

The punching failure of restrained reinforced concrete slabs had been documented as early as the 1960s by Taylor & Hayes [6] and investigated specifically as it relates to bridge deck behaviour in the 1970s by Hewitt & Batchelor [7]. In these and other works, the focus was on the enhancement that arching behaviour provided to reinforced concrete systems. The steelfree deck slab evolved from the philosophy of using the arching behaviour as the primary resistance mechanism. This approach necessitated the enhancement of internal arching forces through a clear and quantifiable in-plane lateral restraint system in both the longitudinal and transverse directions. This restraint is provided by two elements. Firstly, the slab is made composite with the supporting girders, either steel or prestressed concrete. In the longitudinal direction, the large axial stiffness of the girders provides in-plane restraint. Secondly, in the transverse direction, the required restraint is achieved through the addition of external steel straps, normally 25x50mm in cross-section and spaced at 1200mm, which inhibit the relative lateral displacement of adjacent girders. With compression as the dominant mechanism, all internal reinforcement can be removed. Further design details can be found in the design clauses of CHBDC [3] and a recent report of the American Concrete Institute [8]. The essential elements of the system are shown in Figure 1.

In early research, this system was often referred to as a fibre reinforced concrete (FRC) or polypropylene fibre reinforced concrete (PFRC) deck slab due to the use of short randomly distributed synthetic fibres to control plastic shrinkage cracking. In later work, it was referred to as steel-free concrete deck slabs or corrosion-free concrete deck slabs. In the most recent version of the Canadian Highway Bridge Design Code (CHBDC) [3], it is referred to as externally restrained concrete bridge deck slabs. In reporting the research in the following sections, these historical designations have been maintained.

Mechanics Model for Punching Shear Strength

To help develop a reliable theoretical tool for the analysis of bridge decks, the authors re-examined the physical observations made during the experimental program on a variety of steel-free deck models. A more extensive literature review also turned up many similarities between the experimental column punching tests conducted by Kinnunen & Nylander [9]. Kinnunen and Nylander had also proposed an empirical failure criteria based on concrete strains close to the punching zone (referred to herein as K&N failure criteria). Using test observations and the K&N failure criteria, a mechanics model of the behaviour was developed and refined to address additional unique aspects of the externally restrained bridge deck slabs under wheel loads.

Mechanics model formulation

The important components of the system geometry are the depth of the concrete deck, the spacing of the support girders, the spacing and the cross section area of the transverse straps and the dimensions of the loaded area. The essential material parameters are the modulus of elasticity of the material of the transverse straps, the yield strain of the straps, the compressive strength of the concrete, and the 3-dimensional effect on the compressive strength of the concrete under confined conditions.

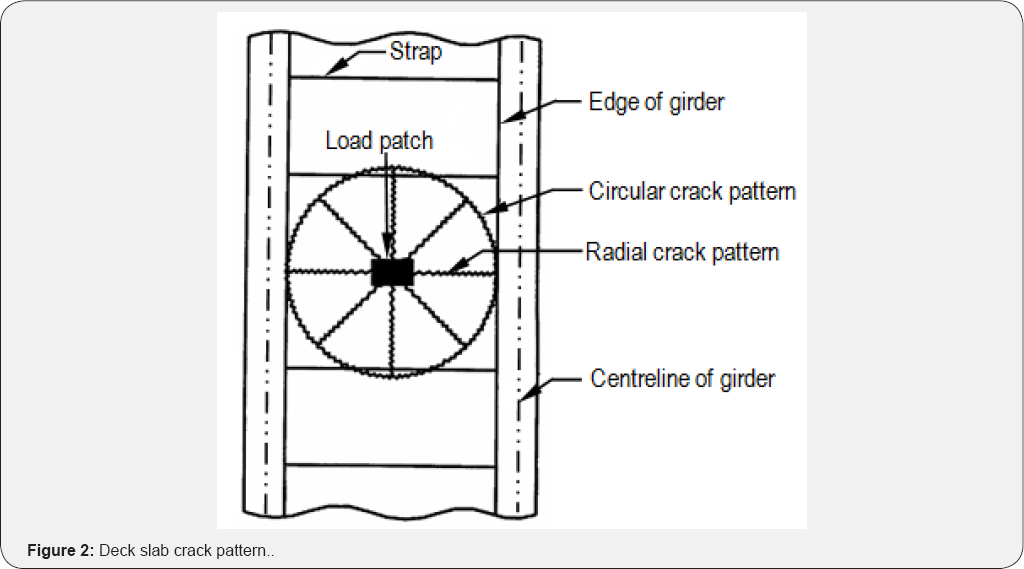
During the initial loading phase, a concrete slab subjected to a concentrated load forms radial cracks on the bottom surface of the slab originating below the load point. As the load increases, these cracks gradually migrate to the top surface of the slab to become full depth cracks (Figure 2). On the top surface of the slab, circular cracks form at a diameter approximately equal to the clear spacing between the girder flanges. As the failure load approaches, an inclined shear crack develops, originating on the bottom of the slab at some distance away from the load point, in a circumferential manner. At punching failure, this inclined crack forms the upper surface of the punch cone. The sections of concrete outside the shear crack can be divided into wedges bound by the shear crack, the radial cracks, and the outside edge of the slab. Under further loading, these wedges act as rigid bodies in the radial direction and rotate about a centre of rotation (Figure 2 & 3).

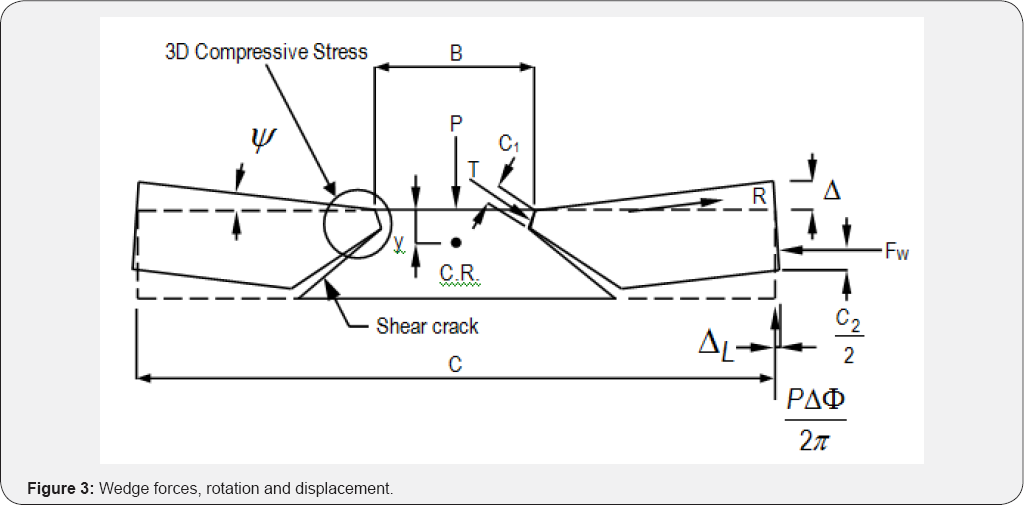
As a wedge shown in Figure 3 rotates through an angle , it has an associated lateral displacement L which is restrained by the stiffness of the straps. If we designate K as the stiffness of the strap, in units of force/displacement per unit length of circumference, then the restraining force is calculated as K L. If we consider a single wedge component, then the forces acting on this wedge are an oblique compressive force acting through the compressive shell and supporting the loaded area T; the vertical support component P Δ Φ /2 ^Π ; the lateral restraining force for the wedge Fw; and a circumferential force R that is developed as the wedge rotates through . The circumferential force R is maximum at the edge of the loaded area. Considering these forces acting in combination with the horizontal component of T and the vertical stress from the applied load, the region near the loaded area is in a state of triaxial compressive stress with σ 1 ≤ ^σ2 ≤ ^σ 3 and ^σ3 = ^a r’^σ 2 = ^σθ and ^σ 1 = ^σ v. Equation 1 is used to model the behaviour of concrete under confinement which enables σ3 to be expressed in terms of 1. As long as the three dimensional state of confinement is maintained around the loaded area, the concrete capacity will remain very high.

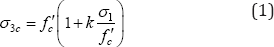
Where, k is a confinement factor (based on comparisons with the experimental punching program, Newhook [10] determined that a value of k=10 was appropriate for the bridge deck application).

Employing the equilibrium conditions and relationships described above, the forces and displacement can be resolved for a given value of applied load P. A complete description of this mathematical formulation is found in Newhook [10]. In addressing the similar problem of the punching of a column slab connection, K & N [9] established empirical criteria for punching failure which was adopted by the authors for bridge deck slab punching. When the circumferential strain at the top surface of the slab close to the loaded area reaches a critical value, ^ϵ ct =0.0019, failure occurs. This value corresponds to the value of strain at the maximum uniaxial compressive stress fc, and the commonly used value of ^ϵ ct =0.002 is adopted. While K&N merely reported this value as an empirical observation, the authors propose that this criterion also corresponds well with the importance of the 3-dimensional confinement of the concrete surrounding the loaded area. Once ^ϵ t equals 0.002, the concrete response softens in that direction leading to a reduction in the confining force, hence punching failure.

The authors also proposed a second parameter that is also capable of initiating punching failure. The lateral restraint is provided by transverse steel straps. The stress in the straps increases with applied load. It is possible that the stress in the straps reaches the yield stress of steel before failure of the concrete occurs. Once the strap yields, it can no longer provide increasing restraint force and hence the concrete will punch under a slight increase in applied loading.

Comparison with experimental work

Comparisons were conducted between experimental failure loads and those predicted by the mechanics model Newhook & Mufti [1]. A partial listing of those comparisons is presented in Table 1. Comparisons of the theoretical and experimental load- deflection and load strap strain results also showed very close agreement [10].

The theoretical model was used to analyze three half-scale tests reported by Mufti et al. [2] and Newhook [10], a deck test on a skew bridge reported by Bakht & Agarwal [11] and full scale testing reported by Thorburn & Mufti [12] and Newhook & Mufti [13]. The experimental deck slabs failed in punching shear and a comparison of theoretical versus experimental failure load is presented in Table 1. The comparison reveals that the mathematical model can predict within reasonable accuracy the punching failure load of internally restrained bridge deck slabs (Figure 4).

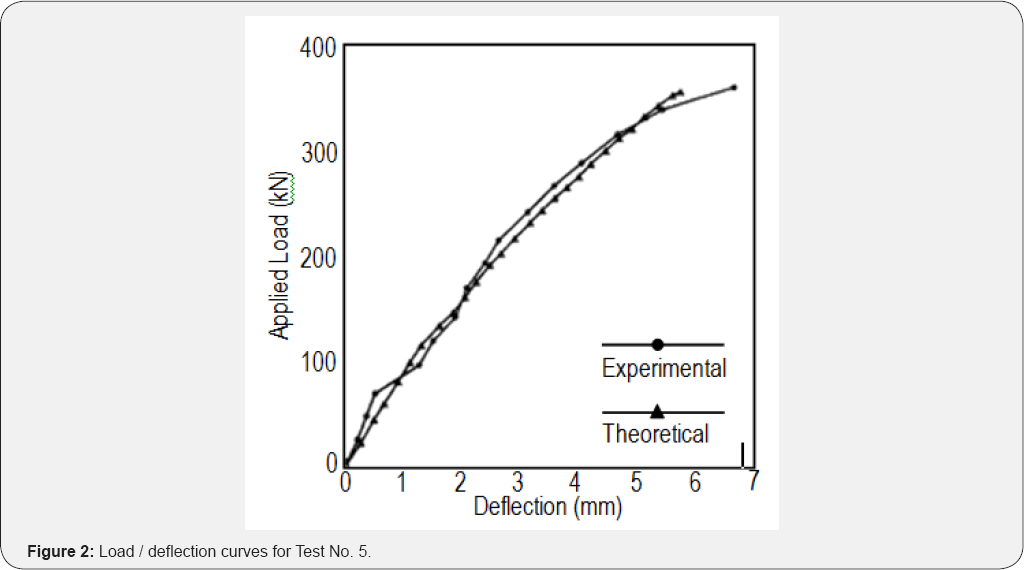
Using the procedure described above, a load deflection curve is constructed for half scale Test No. 5 from Table 1. A small slab displacement is assumed and the associated value of applied is load determined along with strap strain and concrete strain values. If the failure condition is not satisfied, an increment of deflection is assumed and new values determined Newhook [10,14]. This process is repeated until a failure condition is met. Using the values of displacement and load, the theoretical curve shown in Figure 4 is produced. While the experimental curve the theoretical curve though smooth is in good agreement with the observed deflections. The model is reliable in predicting the order of the magnitude of deflection. The experimental deck deflections at ultimate for the tests in Table 1 are compared with theoretical deflections in Table 2. The comparison reveals very close correlation providing further support for the validity of the mechanics model(Table 2)

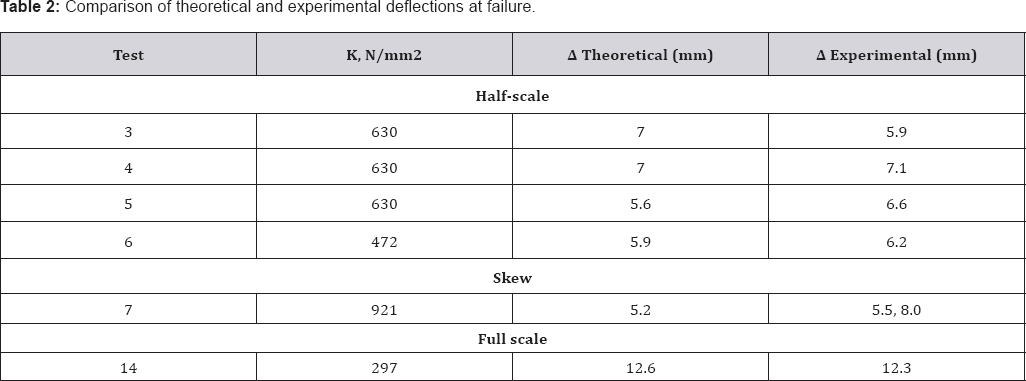
Based on the successful development of this model, the following parameters were confirmed as necessary to properly predict the bridge deck behaviour under wheel load including prediction of ultimate load: deck thickness, girder spacing, strap geometry (restraint stiffness), concrete strength and strap modulus. In addition, strain limits in the strap material and the concrete could be used to define ultimate limit state.

Non-Linear Finite Element Modelling Studies

The initial investigation of externally reinforced bridge deck behaviour was conducted by Wegner and Mufti [15] who attempted to use finite element modelling to replicate the behaviour of the experimental model [2] listed as Test 3 and 4 in Table 1. The commercially available program ADINA (ADINA R&D Inc. 1987) was chosen, since it incorporated a sophisticated tri-axial material model for plain concrete. Specifics of the model and analysis details are reported elsewhere [15,16]. While Wegner and Mufti were able to model the behaviour of one specific test, they concluded that this early finite element modelling attempt was very sensitive to a number of parameters and that extensive calibration with known results and modelling iterations would be required to fine-tune the numerical procedures for a particular application.

The Wegner and Mufti finite element study was conducted prior to the development of the analytical model described in Section 3. This model indicated clearly that for a commercial program to be used successfully the K&N strain limit failure criteria must be used. Hassan et al. [17] conducted finite element analysis of an internally restrained concrete bridge deck slab subjected to wheel loads using the "Anatech Concrete Analysis Program" (ANACAP, Version 2.1) and defining failure as the load at which the K&N failure criteria is met. 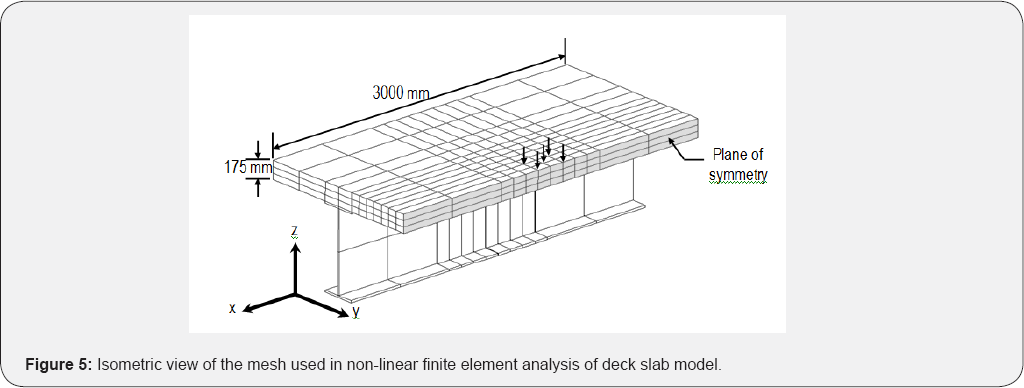One-half of a bridge deck slab was modelled using 20-node brick elements. The slab thickness was divided into three layers. The mesh dimensions used in modeling the deck slab are given in Figure 5. The reinforcement was modelled as individual sub-elements within the concrete elements. Rebar sub-element stiffnesses were superimposed on the concrete element stiffness in which the rebar resides. A complete description of the modeling can be found in Hassan et al. [17] (Figure 5).

Hassan et al. [17] modeled the punching behaviour of a full- scale experimental model of a concrete deck slab on two steel girders tested by Khanna et al. [5]. The experimental model had four segments (Segments A through D) in which the internal reinforcement configuration was varied. Segment A had a top and bottom grid of orthogonal reinforcement, typical of current design practice, and Segment C had just bottom transverse bars. The comparison of the ANACAP theoretical results with the experimental load-deflection results for these two segments are presented in Figure 6a and 6b, respectively. For failure prediction, use of the K&N criteria was critical. With this failure modeling approach, the FEM model proved to be far more robust than the model used previously by Wegner & Mufti [14]. Furthermore, the study confirmed that the presence of top reinforcement in bridge deck slabs has a negligible effect on punching shear capacity (Figure 6a & 6b).

Specialized Non-Linear Fem For Bridge Deck Slabs - Fempunch

The successful use of the K&N failure criteria with a commercial FEM program led to the development of a specialized FEM program for non-linear analysis of externally restrained concrete slab on girder bridges, FEMPUNCH. The program has several features which facilitate the pre-processing and input of bridge geometry. It permits the input of values for the lateral restraint of the straps and includes an orthotropic material model for concrete as well as permits concrete cracking and strain softening and models the benefits of 3-dimensional confinement. It includes the limiting strain proposed by K&N as the failure criteria. The concrete is modelled using a 20-node isoparamteric brick element and the girders are modelled using 2-dimensional beam elements.

FEMPUNCH theory and program

Complete details on modeling assumptions and parameters can be found in Desai et al. [18].

The following assumptions and simplifications have been incorporated into FEMPUNCH:

I. The stiffness of straps is smeared across the length of the girders.

II. Lateral stiffness of the supporting girders is considered to be uniform across the length of the girder.

III. The girders are unyielding in the vertical direction, a simplification that can be remedied easily.

IV. Concrete is modelled as an orthotropic material with the direction of orthotropy being defined by the principal stress directions.

V. Cracking can occur in three orthogonal directions at an integration point used in the formation of finite element equations.

VI. If cracking occurs at an integration point, it is modelled through an adjustment of material properties by considering cracking as a smeared band of cracks.

VII. Strain softening occurs from compression crushing failure to the ultimate strain, at which the concrete fails completely.

VIII. The tensile cracking failure and the concrete crushing failures occur along the principal direction

IX. Load increases monotonically, leading to failure

An isoparametric, 20-node solid brick element has been used in the program to model a bridge deck. At each node, three translational degrees of freedom (u, v and w) are considered. Details of the shape functions and formulation of element level matrices can be found in the literature.

Only one element has been considered in the thickness direction on the basis of the finite element work done by Wegner & Mufti [15]. On the other hand, the number of elements in the longitudinal and the transverse direction is chosen such that the aspect ratio is nearly one. On the basis of the average thickness, the program would select the number of elements automatically between two adjacent sections. However, a user can override this option and feedin the information explicitly.

Modelling of concrete

The 3-dimensional constitutive relations for concrete have been derived from an equivalent, uniaxial constitutive relation, which can be determined experimentally. The uniaxial stress- strain curve has been employed in the program to calculate the tangent modulus.

The stress-strain curve for the concrete has been described by the Saenz's equation [18]. While other 3-dimensional concrete models exist, Saenz's model was selected as it was found to be easier to program and provided equally accurate results. It also avoided singularity problems in the solution process encountered by Wegner & Mufti [15].

Modelling of crack

Tensile failure would occur in concrete when the tensile stress in the principal direction exceeds the tensile strength, ^a f, of concrete. The presence of a crack at an integration point is modelled by modifying the constitutive matrix [18]. When a crack forms, the normal as well as the shear stiffnesses reduce. Consider for illustration that ^σp1 exceeds ^σf.

Solution procedure

The ensuing system level equations are solved in the Lagrangian coordinate system using Newton-Raphson procedure. In-core solution technique has been used to expedite computations. The loads are applied incrementally and iterations are performed per load increment until the solution converges. The incremental displacements and stresses areadded to the values from previous load increments to get the total displacements and stresses. The numerical solution iscontinued until failure occurs.

Comparison with internally restrained deck slab results

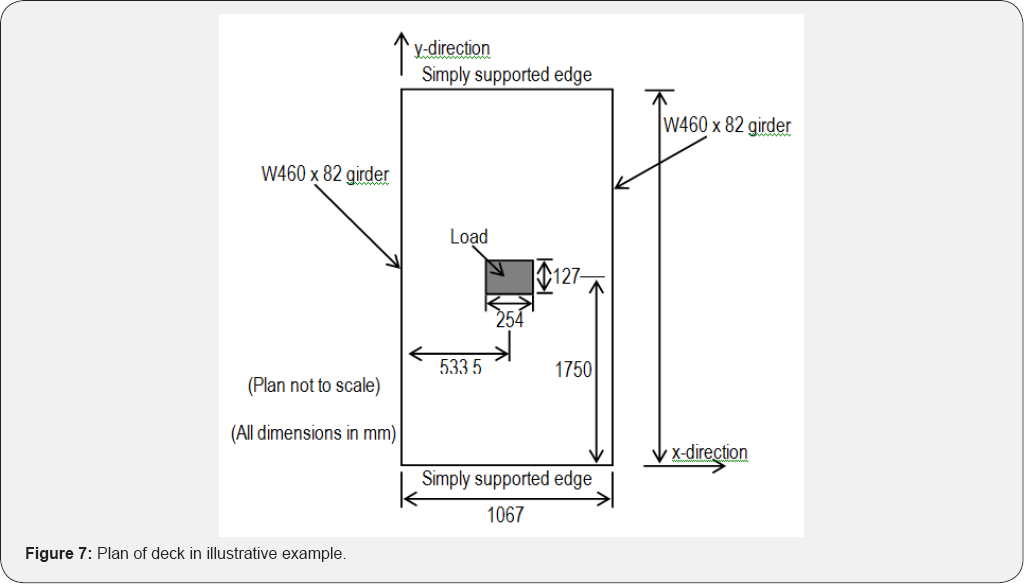
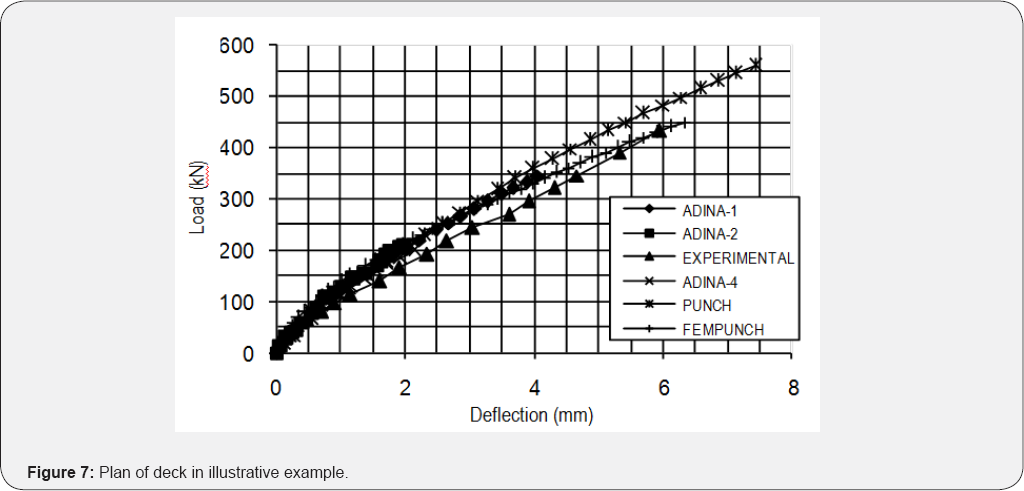
The internally restrained deck slab considered by Wegner & Mufti [15] (Figure 7) has been analyzed using program FEMPUNCH. The load versus deflection under the wheel load results obtained from program FEMPUNCH have been compared with the experimental data, as well as results from the ADINA analyses and results from program PUNCH [14]. It can be seen in Figure 8 that the results from program FEMPUNCH match reasonably well with the experimental data at failure (Figure 7 & 8).

This specialized finite element program incorporates behaviour characteristics and failure criteria developed in the analytical model of Section 3, it also provides several key improvements:

a) Both right bridges and skew bridges can be analyzed;
b) The stiffness of the bridge girders can be modelled;
c) The influence of the global stiffness of the concrete deck outside the punch zone can be included; and
d) The influence of the wheel position relative to the planar geometry of the deck can be modelled.

Further investigations by Klowak et al. [19] demonstrated that the FEMPUNCH program can also be used to predict the response of deck cantilevers to wheel loads.

Conclusion

This paper presents a brief overview of the authors' investigations into modeling the non-linear behaviour and failure of concrete slab on girder bridges to supplement the extensive experimental work in this area. Analytical and specialized finite element tools have been presented. In developing these models, the use of the K&N failure criteria was a key consideration in achieving correlation with experimental results. Both models also allow for the development of a load versus deflection curve for the entire loading not just a prediction of ultimate load. Hence the models, and in particular the finite element, will permit engineers to study the impact of various geometry and material parameters on the behaviour of the deck system. These parameters, in general order of greatest impact on ultimate load, are:

a. Stiffness of the external restraint to the deck including straps and girders;
b. Deck thickness;
c. Girder spacing;
d. Strap material properties; and
e. Concrete strength.

The modeling work also shows that the punching strength of the concrete deck slab cannot be considered a function of just the concrete slab thickness and compressive strength alone but is a property of the entire deck system including the girders and any other means of lateral restraint, in the case external straps.

The punching strength of a concrete slab on girder bridge deck subjected to wheel loads represents a complex problem including both material and geometric non-linearities. To date, no simplified formula has been able to capture the impact of all the parameters discussed in this paper. It is believed that the research presented in this paper will be of assistance to engineers seeking to implement more rigorous solutions and to better understand the influenceof their design choices on the performance of this bridge deck system.

Acknowledgement

The authors acknowledge the contributions to modeling and understanding bridge deck behaviour by the many graduate students and research assistants whose published work is cited herein. The authors also acknowledge the long standing collaboration with our colleague Dr. Baidar Bakht who initially requested that we develop a theoretical model to help understand the behaviour observed during experimental work and who has continued to participate in the solutions.

For More Open Access Journals Please Click on: Juniper Publishers
Fore More Articles Please Visit: Civil Engineering Research Journal