Simulating the Discharge Coefficient of an Improved Triangular Side Weir using a Novel Hybrid Method of Firefly Optimization based Support Vector Regression-Juniper Publishers

Juniper Publishers- Journal of Civil Engineering

Abstract

The discharge coefficient of side weirs is the most important required information in designing side weirs and tributary channels. An accurate discharge coefficient method needs to do a trustable design. The aim of this paper is to introduce and compare the Firefly optimization- based Support Vector Regression (FFSVR) with other powerful artificial intelligence approaches, including Artificial Neural Network (ANN), Genetic Programming (GP) and Support Vector Regression (SVR) to predict the discharge coefficient of an improved shape, triangular side weir. According to the results, the FFSVR model with RMSE of 0.035 performed the best among ANN, GP and SVR, with RMSE of 0.036, 0.040 and 0.039 in the test dataset, respectively. It can be concluded that combining the Firefly optimization algorithm with SVR can produce a higher- performance model.

Keywords: Artificial neural network, Discharge coefficient, Firefly optimization algorithm, Genetic programming, Support vector regression,Triangular side weir

Abbreviations: MLPNN: Multi-Layer Perceptron Neural Network; RBNN: Radial Basis Neural Network; PSO: Particle Swarm Optimization; GA: Genetic Algorithm

Introduction

Side weirs are always used in a wide range of hydraulic structures, including irrigation and drainage systems, diverting and dividing flow structures, as well as flood control utilities. The first study to mathematically describe side weir flow was under taken by De Marchi [1]. The author presented the following equation using the constant specific energy assumption for the upstream and downstream of the side weir.

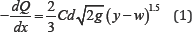
Where Cd is the discharge coefficient, w weir height, flow depth and 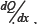variation of discharge with respect to distance along the main channel. The first side weirs that were practically employed had a rectangular shape. Determining the discharge of such side weirs is a topic of interest in many studies [2-7].

For a side weir to pass additional flow, the one option is to increase the side weir length. Increasing the length of the side weir can be done in two ways. One way is to increase the tributary channel width, or second, the side weir shape can be modified.Obviously, the second way is much more economical than the first. Therefore, numerous studies have focused on modifying the shape of side weirs [8-12]. Geometric modification can help increase side weir performance by 1.5 to 4.5 times [13].

On account of the complex nature and various geometric and hydraulic dependencies of discharge coefficient conditions, different soft computing methods are often used as a fast and accurate means of predicting the discharge coefficient [13-16]. The discharge coefficient of the triangular side weir that is considered in the present study is modelled in various studies. Zaji and Bonakdari [17] are modelled the present side weir discharge coefficient using Multi-Layer Perceptron Neural Network (MLPNN), Radial Basis Neural Network (RBNN), and Particle Swarm Optimization (PSO) based equations. Zaji et al. [18] modelled the considered side weir discharge coefficient using a hybrid method of PSO based RBNN. The authors concluded that PSO improved the RBNN prediction performance. By using ANFIS there are two studies in simulating the discharge coefficient of the present side weir [19,20]. The authors concluded that ANFIS has a high capability in simulating the present side weir discharge coefficient.

To enhanceneural network performance, one possibility is to combine the neural networks with optimization algorithms [21-25]. In this study a hybrid combination of Support Vector Regression method with Firefly optimization algorithm (FFSVR) is introduced and compared with three well-known artificial intelligence techniques, namely ANN, GP and SVR. To compare the models, the discharge coefficients of the improved side weir were predicted and verified using a published experimental dataset [26].

Materials and Methods

Experimental dataset

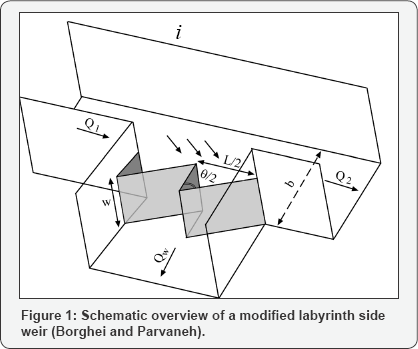
Borghei and Parvaneh [26] experimental dataset for an improved triangular side weir was used to verify and compare the FFSVR, SVR, GP and ANN methods. The authors introduced a new side weir shape that could increase the pass discharge ability up to two times (Figure 1). The experiments were done in a glass channel with 11m length, 0.4m width and 0.66m height.

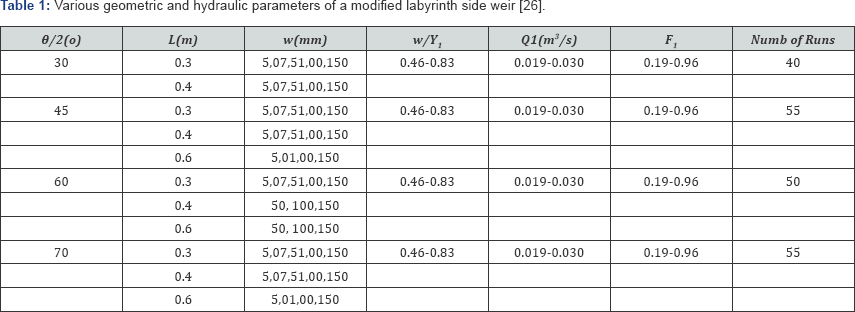
Various hydraulic and geometric conditions were considered in the experimental study. The interval of this verification is shown in Table 1.inth side weir [26].

Numerical models

Artificial neural network (ANN): The back propagation learning algorithm artificial neural network has been widely used in numerous studies. An ANN model consists of three major layers: input, hidden and output layers. Each layer comprises neurons. The neurons of the input and output layers are the input and output variables of the problem, respectively. The back propagation algorithm attempts to determine the weight and bias of each neuron. The neurons in each layer calculate the weighted summation of the last layer's neurons and bias values and place this summation in the transfer function. Neurons can use many transfer functions with the hyperbolic transform function being the most common [14,27,28] and defined as follows:

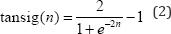
In this study, the input layer consists of the considered non- dimensional parameters of the improved triangular side weir and the output layer is the discharge coefficient. Details of the ANN algorithm are given in [29,30].

Genetic programming (GP): Genetic Programming [31], a subset of the Genetic Algorithm (GA) [32], is a program- based method that uses the symbolic form of programs as chromosomes. The initial population is selected randomly. Each individual of the population is a randomly generated program made from random input combinations, random arithmetic (+, -, x, ÷) and mathematical functions (sin, cos, etc.), and random logical functions (NOT, AND, OR, etc.). By using the fitness function, each individual cost is calculated. Subsequently, the individuals (programs) with the best costs are selected to perform the crossover and mutation process. Crossover is meant to change the parts of two programs with each other and mutation is to randomly change a program to create new programs. This evolution is repeated to achieve the defined stop criterion. The output of the program is a program that could predict the discharge coefficient of improved triangular side weir by using the non-dimensional input parameters. The GP procedure is presented in more detail in [33,34].

Support vector regression (SVR): Support vector regression is a high-performance method capable of handling regression and classification problems much better than other neural networks [35,36]. Most of the other machine learning methods are performed from local training errors in their training process, but SVR uses upper band generalization error minimization in the training process [37]. SVR is described in detail in [38,39]. In this study, an SVR model with RBF kernel function was used to model the discharge coefficient of the improved triangular side weir. RBF kernel function scan handle complex problems more accurately than other kernel functions [37,40]. An RBF kernel function is defined as:

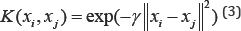
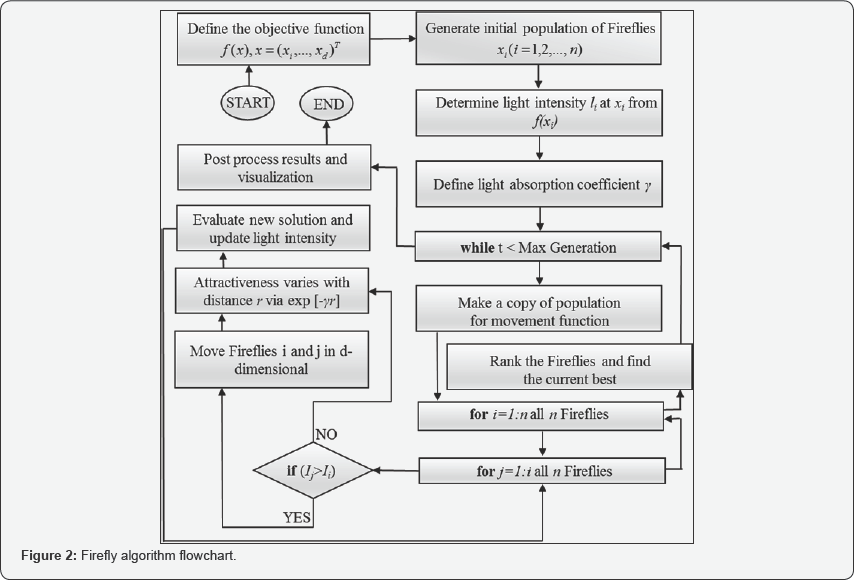
Firefly optimization-based support vector regression (FFSVR): The accuracy of SVR model prediction is directly related to the correct specification of model variables. In this study, the optimal values of SVR variables were determined using the Firefly optimization algorithm [39]. The Firefly algorithm can perform much better in finding the optima compared to other evolutionary optimization algorithms [40-43]. The basic steps of the Firefly algorithm are summarized in Figure 2.

Results

Improved triangular side weir discharge coefficient is related to various geometric and hydraulic situations, such as length (L)) , height (w), weir apex angle (ϕ) , flow depth (y,), upstream Froude number ( F₁ ) and upstream discharge (Q₁) . To run a numerical model to be used in practical and scientific processes without concern about the geometric and hydraulic scales, it is ideal to use non-dimensional input variables. Thus, ten non-dimensional input variables were performed using the efficient variables. Here, the numerical methods FFSVR, SVR,ANN and GP were used to model the discharge coefficient of an improved triangular side weir with the input variables: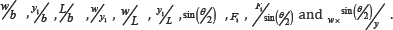

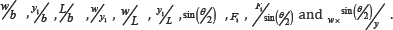
Figure 3 shows the scatter plot and statistic errors of the investigated model for training and testing. From this figure, it can be concluded that the FFSVR model with RMSE, MAE and of 0.035, 0.026 and 4.218, respectively, performed best among the investigated models.

The trend line equation of each model is shown in Figure 3. The form of a linear trend line equation is y = C₁x + C₂ . It is obvious that as C₁ approaches one and C₂ approaches zero,the model is more fit to the experimental results. The figure shows that the FFSVR model with C₁ equaling 0.976 and 0.912 in the trainin and testin data respectively, could predict the improved triangular side weir more accurately.

Figure 3 indicates that for all four models, the performance of training and testing data is very similar. This is indicative that the models were not trapped in over-fitting. Over-fitting occurs when the instruments used to design the model are more than enough. Thus, in an over-fitting situation, the performance of the training dataset prediction is significantly better than the testing dataset.

Conclusion

In this study, the Firefly optimization algorithm was combined with an SVR model to achieve a new, powerful hybrid method, the FFSVR. The performance of the FFSVR was then investigated and compared with the three most applied artificial intelligence methods: SVR, ANN and GP. The output of the models was the discharge coefficient of an improved triangular side weir, and the inputs were ten non-dimensional parameters obtained from the main parameters: w, L ,θ ,y, , b and F_l .The results signify that the FFSVR with RMSE of 0.035 in the test dataset achieved the highest performance among all investigated models. It can be concluded that the Firefly optimization algorithm can be successfully combined with the SVM method to increase the model's ability to predict accurately.

For More Open Access Journals Please Click on: Juniper Publishers
Fore More Articles Please Visit: Civil Engineering Research Journal