Seismic Vertical Component Effects on Seismic Demands of a Base Isolated Bridge with Friction- Rubber Bearings- Juniper Publishers
Juniper Publishers- Journal of Civil Engineering
Abstract
Past experiences regarding the near-fault effect of
earthquakes have shown a potentially significant effect of vertical
component on the response of bridges and their seismic equipment. In
this study, a friction-rubber hybrid isolator was designed for a highway
bridge and modeled to evaluate the effect of vertical seismic component
on the performance of isolators in a concrete bridge. Numerical study
on the bridge was conducted under two conditions:
i. With only two horizontal seismic components, and
ii. With three seismic components (including the vertical component).
For this purpose, finite element model of the
structure was developed in Open Sees software and then subjected to
nonlinear dynamic analysis under 29 different ground motion records. The
results showed that maximum shear and axial force in the isolator
elements undergo significant increase under all seismic excitations. Due
to the absence of self-restoring force in the studied isolator, the
permanent and maximum deck displacement increased during some of the
earthquake records, and in a few cases, the permanent displacements of
the deck were particularly significant. The axial forces of the
isolators on the base and abutment were found to be correlated with the
spectral acceleration at the period of vibration mode effective in
vertical direction.
Keywords: Seismic isolation; Vertical component; Time history analysis; Highway bridge
Introduction
The growth of urban population and industrial
activities and their steadily increasing transportation requirements
have led to a widespread construction and use of highway structures in
and around major cities. Bridges play an essential role in
transportation networks specify after earthquakes. Given the vital role
of these structures in transportation systems, ensuring their safety and
optimal seismic performance is of significant importance. Base
isolation systems can protect the superstructure against earthquake
damage by decoupling it from the substructure and thus from the seismic
load. Such seismic load reduction scheme largely depends on proper
function of isolation units. Thus, factors associated with the
performance of isolators are of significant importance for the seismic
performance of structure and have to be evaluated under different
seismic excitation. Vertical components and strong pulse motion of
ground motions are among the factors that may adversely affect the
performance of a bridge isolation system, especially in near-fault
areas. In particular, this component can undermine the performance of
friction isolators operating alone or in combination with rubber
bearings. In such isolators, variation in axial force between the two
sliding pads may induce instability in the energy dissipation process
and cause erratic isolation performance, and thereby affect the relative
displacement and shear response of the device and structure. Figure 1 shows a friction-rubber hybrid bearing in a bridge with box girder deck.
The effects of vertical seismic component on bridges
with or without seismic isolation systems have been extensively
researched. Some of these studies have emphasized the consequences of
ignoring the vertical component in the nearfault structures. Papazoglou
& Elnashai [1]
have provided both analytical and field evidence supporting the
damaging effects of vertical seismic component on buildings and bridges.
They expressed that significant fluctuation in the axial force of
vertical components leads to a reduction in the shear capacity of
columns. Gloyd [2]
developed a design criteria by studying 60 pre stressed box girder
bridges with due attention to the effect of vertical seismic component.
Design values considered for the vertical shear force in deck and
flexural moment in two main spans of these bridges indicate that dynamic
response induced by vertical acceleration is much larger than the
effect of dead load. Kunnath et al. [3]
the effect of vertical seismic component on the seismic design
recommended by Caltrans (Caltrans Seismic Design Criteria) regulation
was investigated on multiple conventional bridges. The results of this
study showed that Caltrans regulations have a poor accuracy and cannot
account for the changes made by the vertical ground motion component in
the axial force of column and the mid-span moment. Rahayi &
Arezumandi [4]
studied the effects of vertical seismic component on the bridge piers
using the seismic records of Tabas 1978, Northridge 1994 and Kobe 1995
earthquakes. They reported that the presence of vertical component
increases the axial force as well as axial and shear strain, but the
consequent changes in shear force and longitudinal displacement are
negligible. However, due to absence of seismic isolators in the
structures examined in the aforementioned studies, their results cannot
be relied upon to explain the seismic behavior in the presence of
isolators.
A number of researches have focused specifically on
the effect of vertical seismic component on the isolator behavior. For
example, Naeim & Kelly [5]
investigated the relationship of horizontal and vertical stiffness with
vertical load and lateral deformation respectively, and reported that
increase in vertical load and lateral deformation leads to a decrease in
vertical and horizontal stiffness respectively. Nakajima et al. [6]
using experimental model and numerical analysis examined the effects of
vertical seismic component on the bridge piers equipped with isolation
systems. Considering the effects of vertical seismic component on the
variation in the axial force of isolator component, they reported that
these changes have no significant effect on response values.
Nevertheless, they emphasized that when evaluating the performance of a
base isolated bridge under vertical seismic component, changes in the
friction coefficient should be duly considered. Iemura et al. [7]
studied the effect of vertical acceleration on the seismic performance
of Japanese highway bridges under four seismic events. The results
showed that vertical seismic component has a substantial effect on the
response of isolation systems. In a study by Mazza & vulcano [8]
on the response of a building resting on different hybrid isolators and
subjected to all three seismic components, it was found that due to a
longer natural period, the adoption of a friction- rubber system proves
effective for controlling the damage of RC frame members. However, these
researchers did not investigate the behavior of such systems affected
by ground motions with significantly large vertical components. Warren
et al. [9]
investigated the effect of vertical seismic load on the low damping
lead-rubber bearings in bridges, the results showed that vertical
stiffness of isolation systems should not be ignored. In another study,
Reyhanoøullari [10]
studied the effect of vertical seismic component of seven accelerogram
records on steel bridges with and without base isolation. They used
numerical model of leadrubber bearings in the study. The results of this
study showed an increase in responses and their correlation with
defined criteria. Wang C et al. [11]
investigated the effects of vertical excitation on the seismic
performance of a seismically isolated bridge with sliding friction
bearings. Different bearing friction coefficients and different
stiffness levels (pier diameter) were discussed in the paper. The study
results showed that vertical excitation had a relatively large impact on
seismic performance for a seismically isolated bridge with sliding
friction bearings where vertical excitation dominates.
Review of aforementioned studies shows the importance
of the vertical component effects on behavior of base isolated bridges
and absence of a detailed investigation on the seismic behavior of
hybrid friction-rubber isolators under seismic excitations with
significant vertical component. To address this issue, in this paper, a
numerical model was developed to investigate the performance of the
structure by nonlinear time history analysis.
To determine the relationship of vertical
acceleration with the axial force of isolator, the relationship between
the response values and their corresponding spectral values along
vertical direction was investigated. Moreover, since the seismic
performance of a bridge largely depends on the performance of its
seismic equipment, the effect of vertical earthquake component on the
seismic response of hybrid isolator was studied. To find out the
mentioned relationship and the performance of the isolator, first, a
friction-rubber hybrid isolator was designed according to the AASHTO
(American Association of State Highway and Transportation Officials,
Guide Specifications for Seismic Isolation Design, 2010) recommendations
[12]. A threedimensional model of the bridge was then developed in the finite element Open Sees software [13].
Finally, the effect of vertical seismic components on the response
parameters of the bridge and isolators was investigated under two groups
of dynamic analysis: A group with only two horizontal seismic
components; and another with two horizontal along with vertical
component.
Bridge Specifications and Numerical Model
For the purpose of numerical study, a continuous
bridge consisting of two 25-meter spans. The deck was employed includes 5
girders and a concrete slab of 20cm thickness. In addition, the single
pier comprises of 3 columns with beanshaped cross-sections connected to
the cap-beam. The girders attach to the abutments and middle pier using a
concrete diaphragm to allow for an integrated performance. Three
isolators are installed in each of the abutments as well as the middle
pier below the concrete diaphragm on the cap-beams. The soil-structure
interactions in the foundation and abutment were ignored. The main
components of the bridge and its isolated view are illustrated in Figure 2. In this study, an elastic a stick model was employed to simulate the bridge deck [14].
The command "Uniaxial Material Concrete01" was used to model the
confined concrete, as well as the cover or unconfined concrete.
This command for uniaxial concrete materials utilizes the degrading
linear unloading/reloading stiffness model developed by Kent and Park [15,16].
In unconfined concrete, strain is taken as 0.002 and 0.006 for maximum
strength and crushing strength, respectively. In Confined concrete,
strain of 0.005 and 0.05 occur
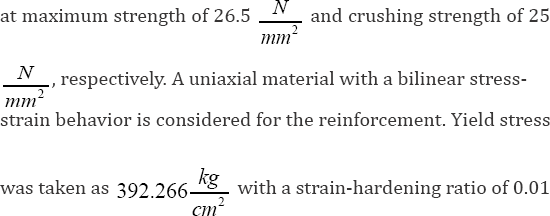(Figure 3)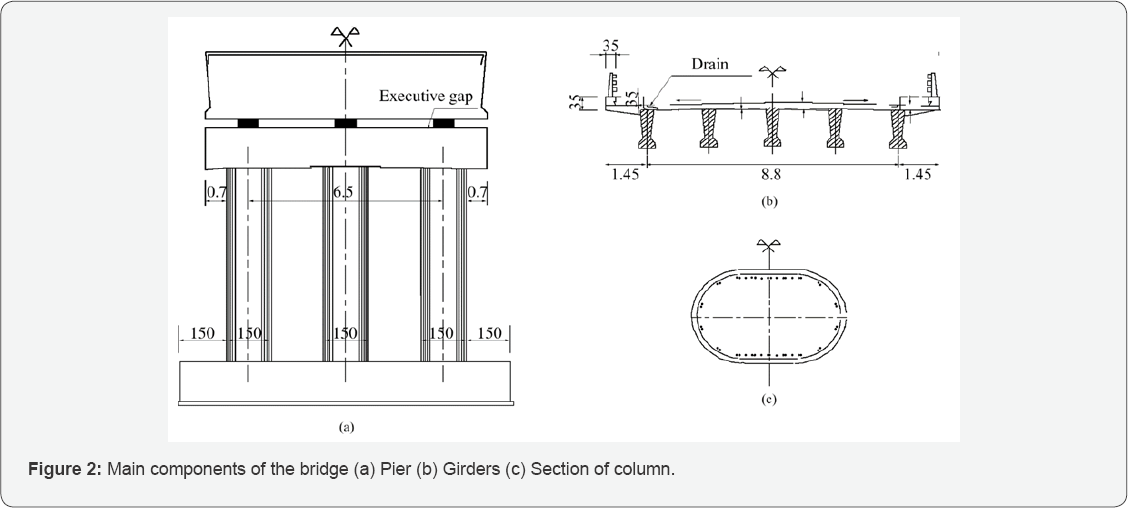
The isolator consists of a rubber bearing attached to
slider steel plates whose contact surface is coated by
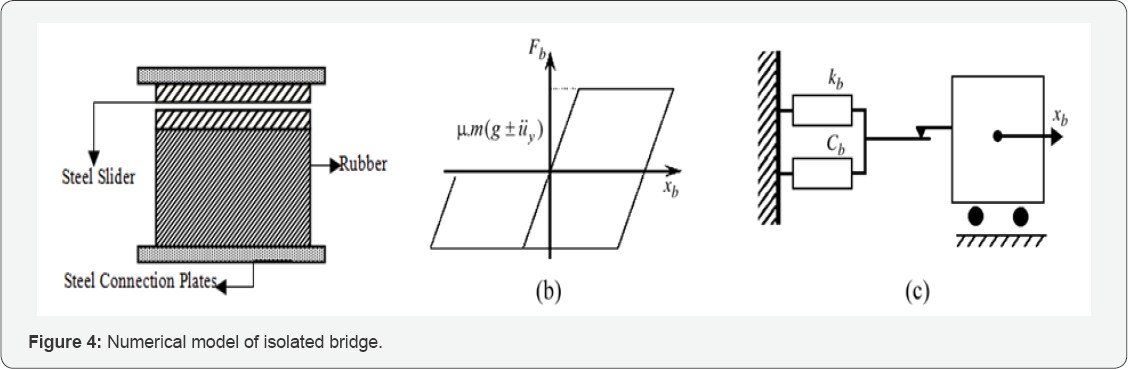
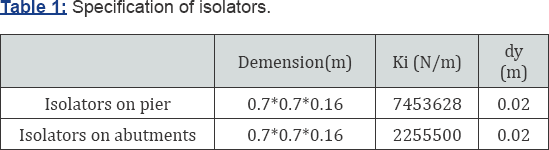
Polytetrafluoroethylen (PTFE). Figure 4a
demonstrates the logic model and nonlinear behavior considered for the
isolators. A schematic view of the hybrid isolators employed in this
study is shown in Figure 4b.
The initial stiffness in nonlinear behavior of device is provided by
rubber pad which deflects until the restoring force reaches the limit
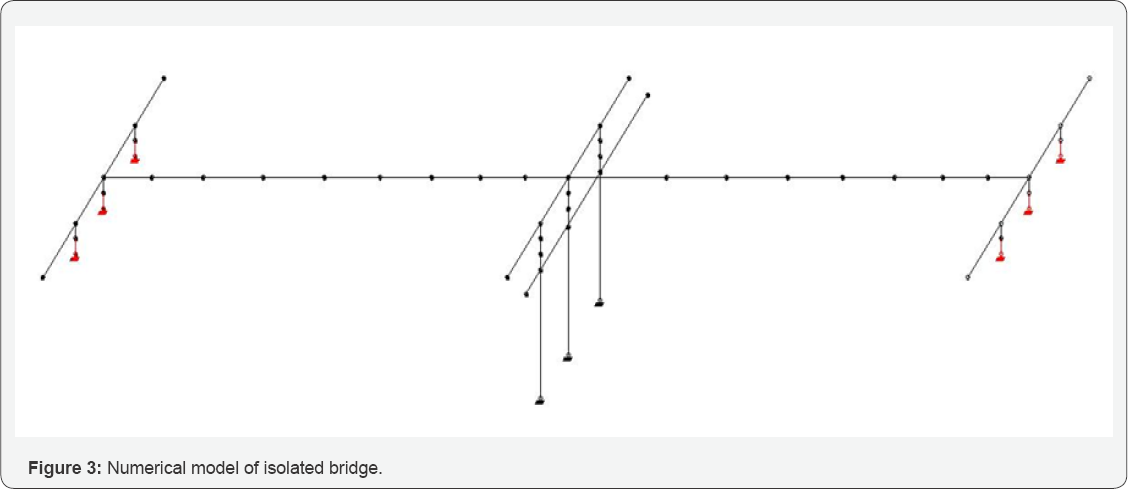
required for the slider part to move. Equation 1 describes the friction
force (Fb) as a function of mass, gravitational acceleration and ground vertical acceleration at the time of earthquake. (Figure 4c)
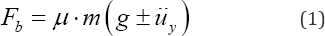
Two types of these isolators were designed, the specifications for which are given in Table 1.
The sliding velocity and instantaneous vertical force
applied to the isolators change. Consequently, the vertical force or
vertical acceleration directly affects the shear force acting upon the
isolator. On the other hand, changes in both sliding velocity and
instantaneous vertical force parameters cause variations to the
coefficient of friction, which in turn changes the shear force. Hence,
the proposed behavior model by Dao was used to model the coefficient of
friction [18].
In this model, the coefficient of friction was experimentally
calculated for different sliding velocities and 8 different vertical
forces. Then, as demonstrated in Figure 5,
the curve fitting was carried out based on the results. The coefficient
is expressed according to Equation 2 as a function of the obtained
minimum and maximum values [19].
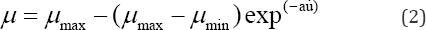
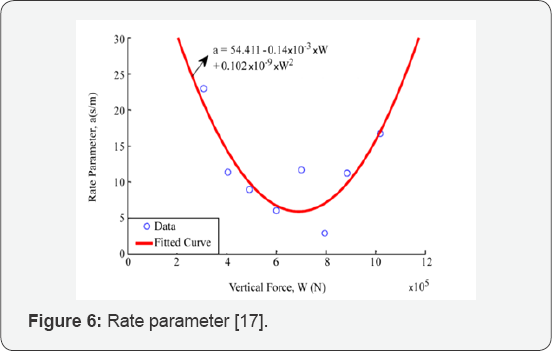
Where, is the instantaneous velocity and a is an
empirical parameter depending on the applied pressure as well as the
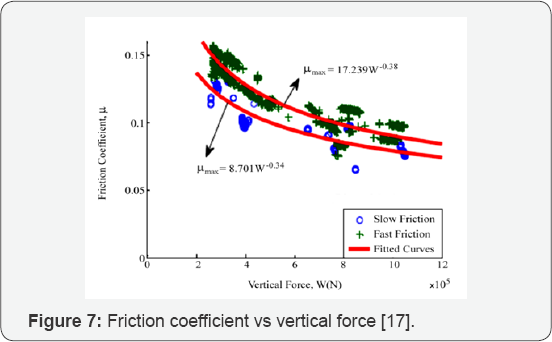
conditions of sliding surfaces (Figure 6). Additionally, μmax
and μmin are the values of coefficient of friction obtained
at maximum and minimum sliding velocities, which vary based on the
vertical force. Variations in these two parameters were expressed by
Bowden and Tabor through Equations 3 and 4, a diagram of which is
depicted in Figure 7 [20].
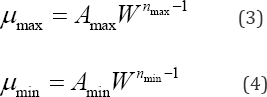
Where Amax and Amin
are constants, and nmax and nmin
are empirically obtained coefficients with values smaller than 1.
Buckling
The relationships needed to check and control buckling of rubber are provided by Naeim & Kelly [5]. The critical vertical load that can be sustained by an isolator can be obtained from Equation (5).
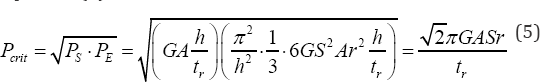
Where PS is the shear stiffness per unit length of the
isolator, PE is the Euler buckling load, G is the shear modulus, A is the cross s ectional area, S is the shape factor (for a square seat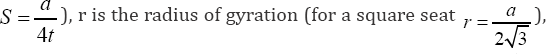 
h is the total height of the isolator (rubber and steel tr), and is the total height of rubber.
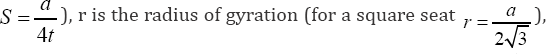h is the total height of the isolator (rubber and steel tr), and is the total height of rubber.Seismic Input
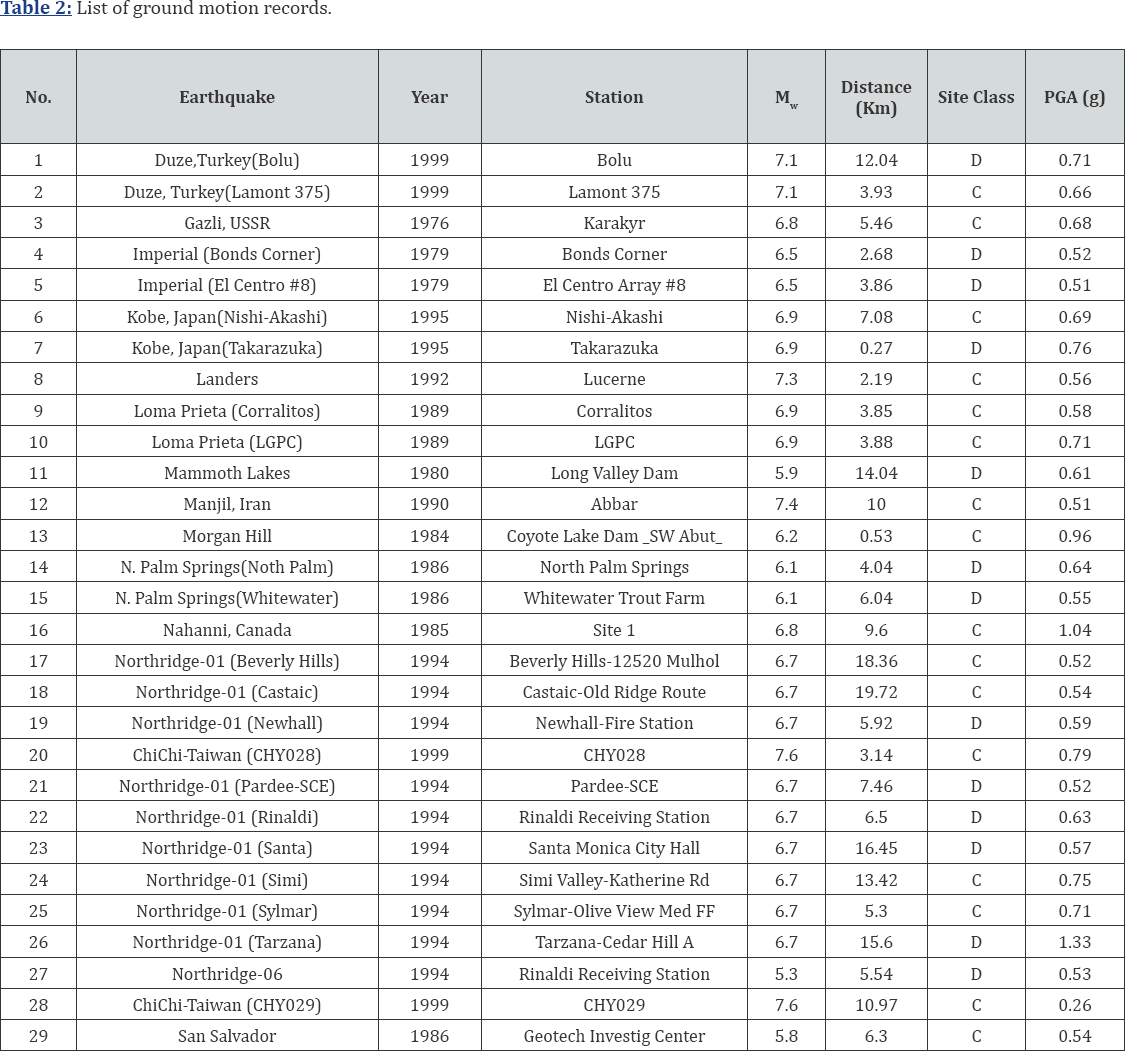
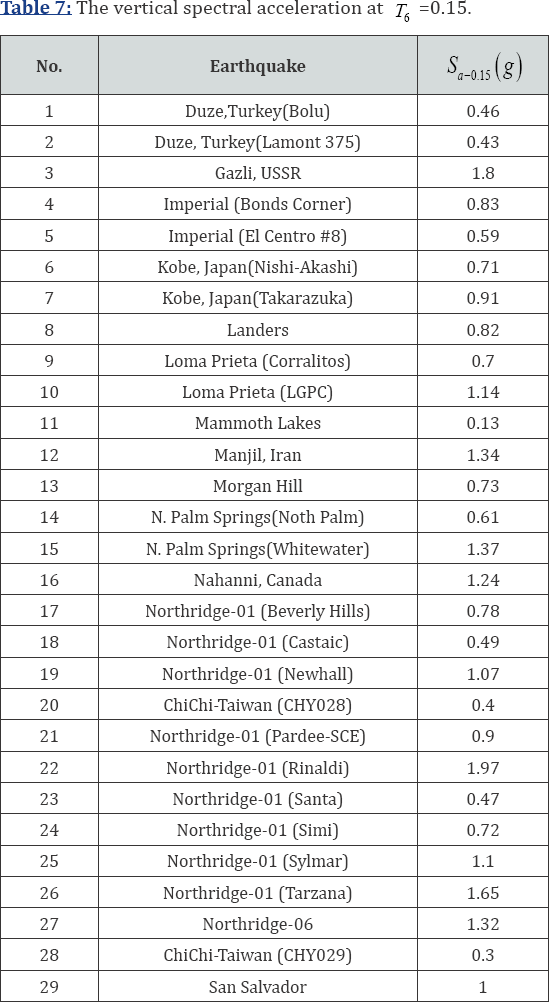
In this study, 29 earthquake acceleration records with considerable vertical components were selected from [21]. Specifications of the accelerograms applied in this study are given in Table 2.
Validation
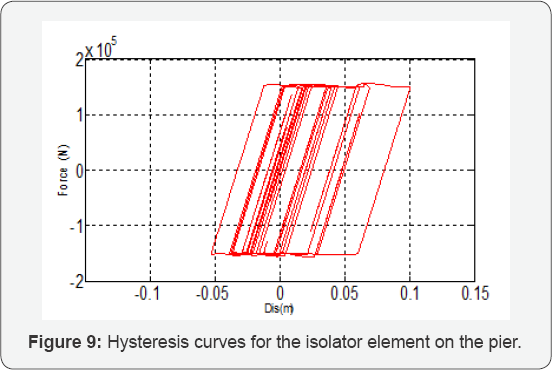
As can be seen, the differences between force and
displacement values obtained from the model and analysis are reasonably
small and can verify the validity of the model. Figures 9 & 10
show the force-displacement curves of the isolators i seated on the
base and the abutment, which were obtained from numerical analysis of
the bridge subjected to the Imperial Valley-06 (Bonds corner) ground
motions applied along its transverse direction. The yield displacement
and isolator shear 1 force are also shown in the Figure. The validity of the modeled 1
isolator was verified by comparing the response with the input data.
The input yield displacement (dy), initial stiffness (Ki), and sliding
force (Fy) values and the analysis results are given in Table 3.
Since design and input data, were determined by assuming a constant
friction coefficient, validation was performed using the Coulomb
friction coefficient.
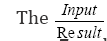ratio of Ki, dy and Fy
for the isolator on the pier is 1 , 0.97and 0.98, respectively. The
corresponding values for the isolator on the abutment is 1. An
acceptable performance of the numerical analysis is observed in the
analysis results shown in Table 3.
Results of Numerical Analysis
Modal analysis
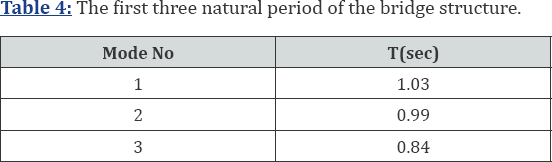
Modal analysis was performed and the natural dynamic
characteristics of the structure were calculated. The first three
natural periods of the structure are presented in Table 4.
Nonlinear time history analysis
The effect of vertical seismic component on the base
isolated bridge was investigated by computing the maximum response under
two following conditions:
i. 1-Under only two horizontal seismic components (without the vertical component)
ii. Under the three seismic components (two horizontal and vertical)
At each stage, the maximum response parameters under
the above-mentioned condition were calculated and the effects of
presence of vertical component on the response values were
measured by the parameter αR , which is defined as:
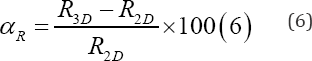
Where, R3D is the maximum response obtained from time history analysis in the presence of vertical component and R2D
is the corresponding maximum response in the absence of vertical
component. The response parameters evaluated under vertical component
are listed in Table 5.
The isolators on the abutment and deck have been indicated by Iso-A and Iso-B, in Figure 3,
respectively. In the following the results for each response parameter
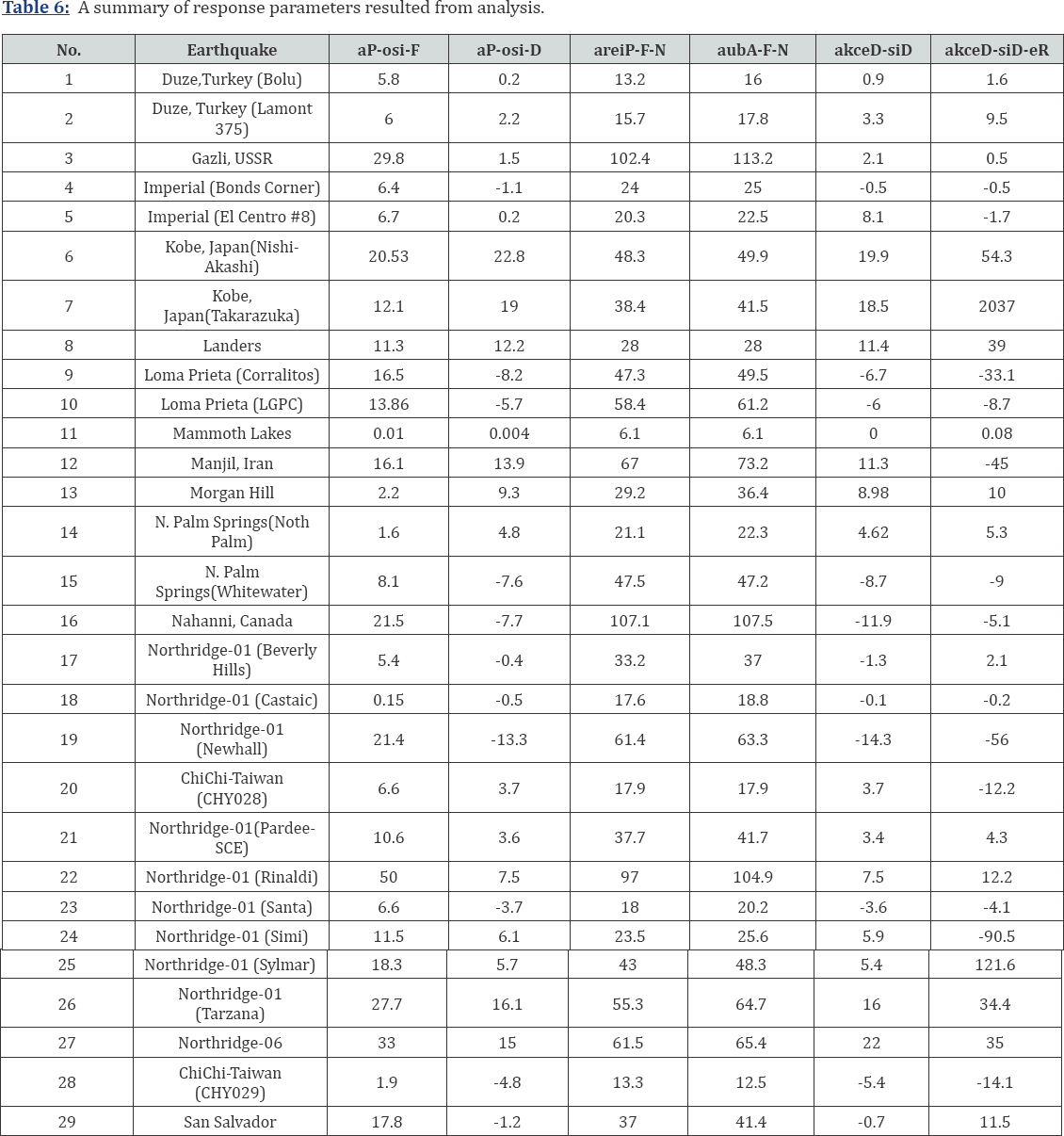
have been discussed. In addition, summary of response parameters has
been presented in Table 6.
Effect of Vertical Seismic Component on the Isolator
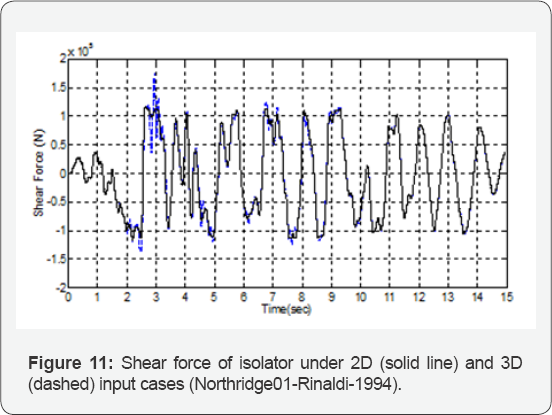
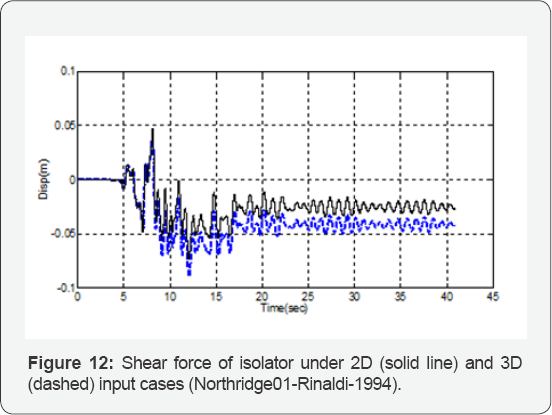
The increase in the maximum values of the shear force
and relative displacement of the isolators under each seismic
excitation as α F-Iso-P and α D-Iso-P are presented in Table 6.
The time history diagrams of shear force and relative displacement of
the isolator on the pier under the Northridge 01 (Rinaldi-1994) and
Kobe-Japan (Nishi Akashi-1995) ground motions are shown in Figure 11 & 12.
According to Table 6,
under all ground motions, the presence of vertical seismic component
increases the maximum shear force. Thus, ignoring the vertical seismic
component in the analysis means utter disregard to the increase in the
isolator's shear force, which may reach as high as 50% under a ground
motion similar to Northridge-01 (Rinaldi). The results obtained under a
number of ground motions also show an increase in the maximum relative
displacement after introducing the vertical seismic component. The most
severe case in this regard is the 23% increase in this response
parameter under the Kobe (Nishi- Akashi) ground motions.
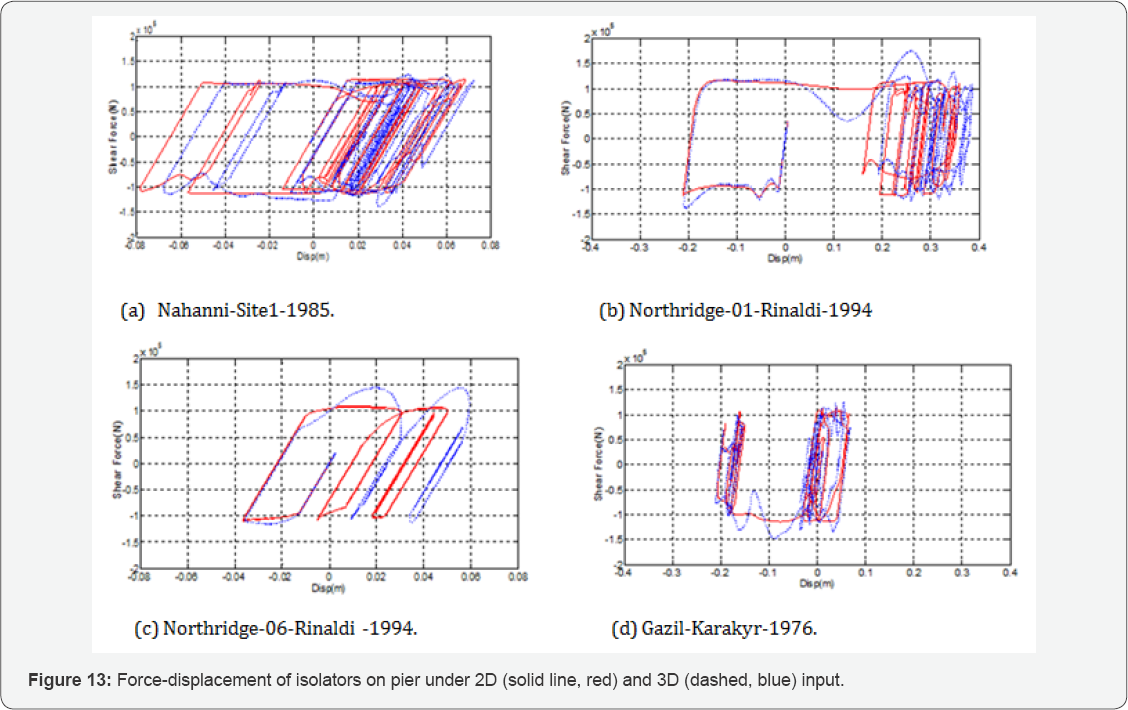
For better evaluation of isolation performance, the
forcedisplacement graphs of base isolators on the pier subjected to four
different earthquake records are presented in Figure 13.
As can be observed, the presence of vertical seismic component is
generally similar, but sometimes the presence of vertical seismic
component has caused a significant increase or decrease in the shear
force. This change in shear force is due to momentary changes in the
friction coefficient and axial force. This is induced by variation of
vertical acceleration. In the presence of vertical seismic component,
axial force of the base isolator undergoes wide-range changes. For
example, the minimum and maximum axial forces obtained under the
Gazil-Karakyr-1976 ground motions are 25KN and 3,035KN. The response
values under Northridge-01-Rinaldi-1994 earthquake record are 273KN and
3,026KN, respectively. These Figures indicate a 120 times increase in
axial force under the former ground motions and an 11 times increase in
this force under the latter case, which are all reflected in the
occasionally erratic changes in the plots of Figure 13 & 13. Figure 13
also shows a permanent displacement in the isolator under the
Northridge-01-Rinaldi ground motion, which is evident from its curve
moving rightward.
Comparing the maximum shear force of the base isolator under the 3D ground excitation with the design sliding force. Table 3
shows that under the Northridge-01-Rinaldi ground motions, the maximum
actual shear force in the isolator exceeds the sliding force considered
for the isolator in the design. For the isolators resting on the
abutment, the calculated maximum shear force in all earthquakes except
Manjil-Iran exceed the design value. This reflects the greater magnitude
of the force transferred from the superstructure to the substructure
and the force at which the deck slides over the isolators compared with
the values considered in the design.
As mentioned in the introduction of AASHTO (2010),
the vertical seismic component is ignored in design process. To
investigate the effect of vertical seismic component on axial force of
isolators, the change of this force due to introducing the vertical
component is calculated. The α-N-F-Pier and α-N-F- Abu parameters for
the isolators seated on the mid-span base and the abutments are shown in
Table 6.
As shown in Table 6,
introducing the vertical components of earthquake have made significant
changes in the axial force. This doubling of the axial force in
isolators indicates the possibility of buckling-induced instability of
devices. The parameter then must be controlled according to Equation 5.
It can be observed that α-N-F-Pier parameter reaches about 107% in
Nahani, Canada earthquake. α-N-F-Abu also increased to 113% in Gazli,
USSR earthquake. To demonstrate the effect of vertical component of
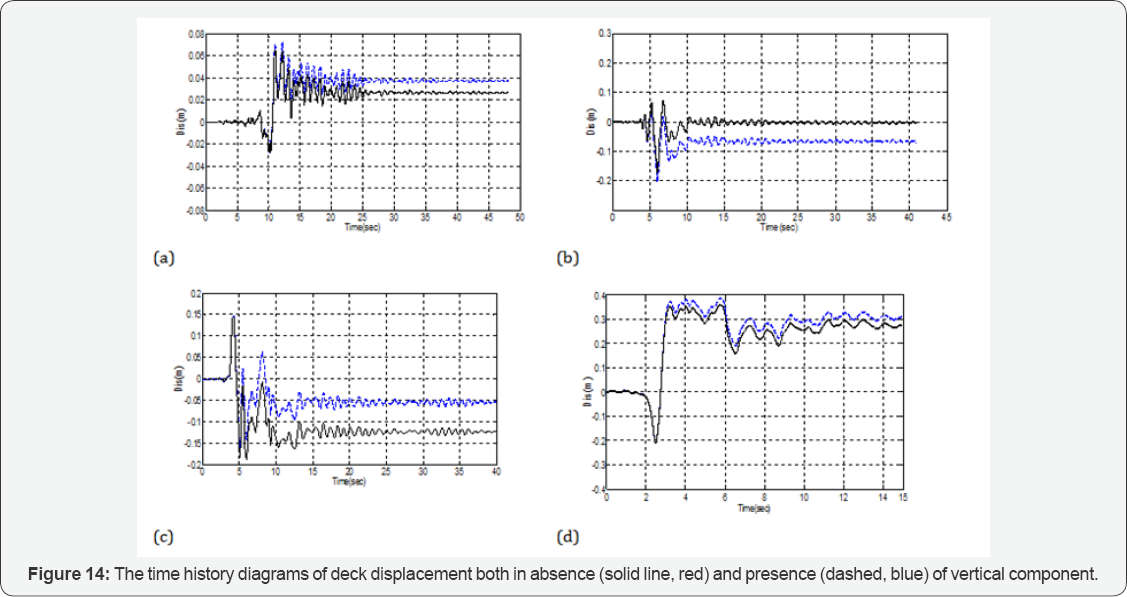
earthquakes on the lateral and permanent displacement of the deck, the
time history diagrams of deck displacement both in absence and presence
of vertical seismic component of four ground motions are plotted in Figure 14.
Appearance of larger residual displacement when the vertical component
is applied, can be observed at the end of displacement time histories in
these Figures. Considering the flexible behavior and partly-
irreversible displacement of friction-rubber isolators, the maximum
horizontal displacement and permanent displacement of the deck in the
absence and presence of vertical seismic component were investigated.
The results obtained from this investigation are presented in Table 6.
According to the data Table 6,
shows an increase of both permanent and transient deck displacement in
some case. This means that, absence of vertical seismic component in the
analysis may result in underestimating the horizontal and permanent
displacement of the deck. Comparing the values of a D-Iso-P and a
Dis-Deck shows that presence of vertical seismic component affects the
deck displacement more strongly than it does the relative displacement
of isolator. The results show that introducing the vertical seismic
component of Northridge-06 (Tarzana) ground motions has increased the
deck maximum lateral displacement by 22%, while introducing the vertical
seismic component of Kobe-Japan (Takarazuka) earthquake has increased
the deck permanent displacement by more than 2000%. A significant
sliding in the bridge deck also can be observed at the moments of sharp
increase in the vertical seismic component (which usually coincides with
a sharp increase in the horizontal acceleration). Due to absence of any
self-restoration mechanism in the sliding part of the device, such
earthquake- induced displacements are permanent. For example, Figure 14
shows that the maximum permanent displacement induced by the
Northridge-01 (Tarzana) ground motion is about 40 cm, which undermines
the post-earthquake serviceability and utility of the bridge.
Spectral Analysis and Correlation of Data
The natural vibration mode with a significant effect
on vertical direction was identified. The correlation of the response
parameters with the spectral values of vertical ground motion component
at the period of this significant mode was evaluated. The response
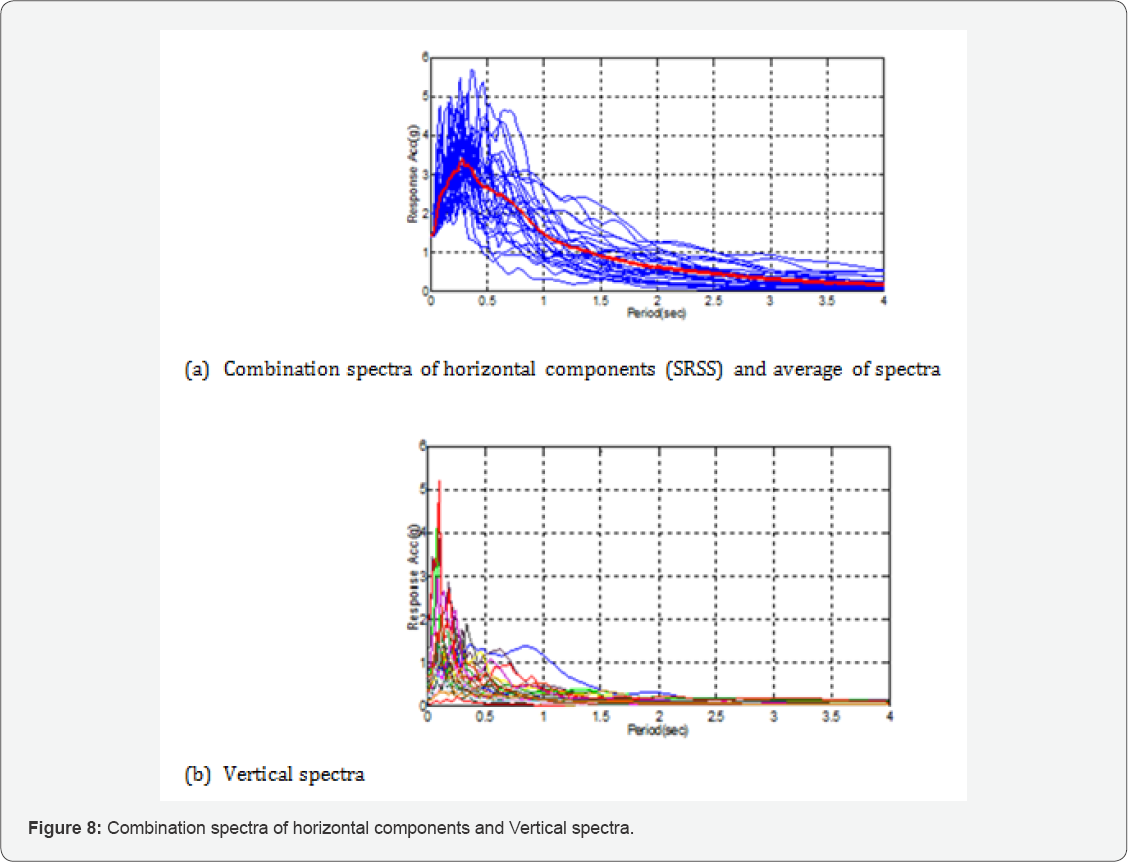
spectra of vertical component of all 29 ground motion were already
depicted in Figure 8. The effective vibration mode of the model in vertical direction is the sixth mode with a
period of T6 =0.15 sec. The spectral acceleration at =0.15 sec
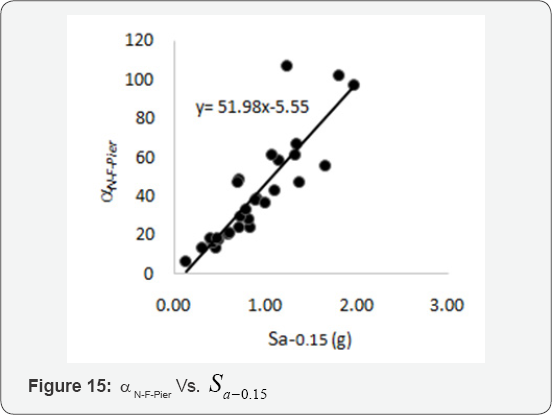
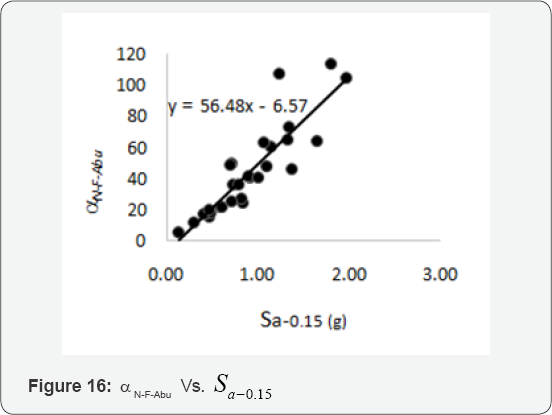
( Sα-0.15) obtained under 29 ground motions are given in Table 7. The α N for the axial force of the isolators on the pier and
abutment, as a result of changes in Sα-0.15 are show in Figure 15 & 16, respectively.
A linear regression can be reasonably applied to the
data. Having the resulted regression equations and Equation 6, the
result of response parameters including the effects of vertical motion
can be estimated.
Conclusion
Despite the significant effect of vertical seismic
component on the performance of isolation systems and structures located
in near-fault areas, some of the design guidelines and regulations
ignore the effect of this component on the base isolated structures. In
this study, AASHTO (2010) guidelines were used to design a
friction-rubber isolation system for a 51m long two-span highway bridge.
The structure was modeled in the OpenSees software. The method
developed by Dao was then used to ensure the accurate modeling of
friction coefficient changes versus the changes in vertical force and
sliding velocity. To investigate the effect of vertical seismic
component on the base isolated bridge, deck permanent and transient
displacement and axial force demand on the isolator device was
investigated. The analysis under 29 seismic excitations with significant
vertical components once with isolator and again without isolator was
performed.
The results obtained from the analysis are concluded as follows:
Ignoring the vertical seismic component in the
analysis means potentially ignoring up to 50% increase in the maximum
shear force.
As observed in Table 3,
when introduced to the model, vertical seismic component caused the
shear force to exceed the values specified in the isolator design
guidelines. This means the force that will be transferred from the
superstructure to the substructure and the force at which the deck may
slide over the isolators may be greater than the design values.
The force-displacement curves obtained once in the
absence and again in the presence of vertical seismic component,
occasionally exhibit some differences due to momentary but considerable
changes in the friction coefficient or axial force.
Vertical component of all tested ground motions
increased the axial force of isolator, sometime by up to 100 percent.
The magnitude of increase highlights the importance of incorporating the
effect of vertical seismic component into the isolator design. Despite
the significant increase in the maximum axial force, isolator models in
this study showed no sign of buckling.
Introducing the vertical component of ground motion
records in some cases increased the relative displacement of the
isolators and horizontal permanent and transient displacement of the
deck.
The axial forces of isolators were found to be
correlated with their corresponding spectral acceleration of vertical
acceleration component and a correlation relationship was derived
accordingly for the system under study.
Acknowledgement
This research was supported by International
Institute of Earthquake Engineering and Seismology (IIEES). This support
is gratefully acknowledged.
For More Open Access Journals Please Click on: Juniper Publishers
Fore More Articles Please Visit: Civil Engineering Research Journal
Fore More Articles Please Visit: Civil Engineering Research Journal
Comments
Post a Comment