Drift Response of Irregular Lightly Reinforced Concrete Frames in Low Seismic Zones- Juniper Publishers

Juniper Publishers- Journal of Civil Engineering

Abstract

The drift response of lightly reinforced concrete frames in low seismic zones is studied in this paper. The frames under study comprise vertical and/or plan irregularities and are designed for only gravity loads as in a low seismic zone. Nonlinear time history analysis using scaled ground motions is the selected approach for this study. Drift is a major consideration in any seismic hazard analysis. Thus, damage levels are addressed according to [1] definitions by comparison of drift responses. The maximum drifts are classified according to the number of story and type of irregularity. A comparison between results of models demonstrates that the drift levels under low seismic intensity are in range of low to moderate; however, the severity of drift is more for most of two story models.

Keywords: Irregularity; Lightly reinforced concrete; Low seismic; Asymmetric plan; Soft story; Time history analysis; Drift

Introduction

There in forced concrete (RC) structures that do not comply with seismic provisions usually are referred to as Lightly Reinforced Concrete (LRC), and mostly were designed with earlier editions of building design codes [2]. LRC structures comprise the majority of RC buildings in majority of low to high intense seismic zones [Ibid.]. In low to medium seismicity zones, such as in the Northeast of the United States (US), RC structures were basically designed for gravity loads only [3] where reinforcement and details of RC structures do not comply with modern seismic standards. However, they may still hold some degree of inherent lateral strength capacity primarily due to applied safety factors, higher material strength, and so.

Besides, inventories of multi-story RC buildings in the US where the architectural design have largely applied irregularities are significant. Combination of "soft first story" and "asymmetric plan" when they combine can be found both in seismic and non- seismic zones. Almost all codes and building standards put on restrictions for irregularities, especially in high seismic zones. The code provisions for torsion and elevation irregularities are derived mostly from elastic studies or from simplified inelastic studies. Structural irregularity consists of irregular distribution of stiffness, strength, and mass within the structure height and/or plan. However, research is rare in taking both vertical and plane irregularities in one structure into account and studying their side effects as a whole response. Almost all research focus on vertical or planar irregularity individually. A review of De Stefano and Pintucchi [4] study regarding major irregular research may explain the aforementioned statement of insufficient amount of study into vertical and plane irregularities. Lack of appropriate code definitions for combination of both plan and vertical irregularities is another issue. Furthermore, structural system irregularity does not depend exclusively on structural properties, yet the ground motion characteristics and the distortion in structural properties shall be stipulated [5]. Response of irregular LRC structures in low seismic zones has been presented before by Rezavandi and Fu [6] which covers the damage stage and number of formed hinges. The former study addressed damage levels associated with hinge formation, while the current study is focused on drift results.

The Eastern and North eastern areas of the US are usually accepted as low seismic zones. ASCE 7-10 [7] defines the Seismic Design Categories (SDCs) from A to F. In the Eastern and North eastern areas of the US, SDCs B and C are the most common hazard categories with some higher and exceptional categories toward the Central US [8]. In this part of the continent, there are infrequent and low to moderate scale seismic activities. For example, the August 2011 earthquake in Virginia was a moderate to low magnitude seismic event. However, total damage estimated to be about $300 million in total and spread over a large area [9].

Drift is a key element in seismic design of new buildings [e.g.7] or retrofit ofthe existing structures [10]. As mentioned before, lack of enough study in the low seismic zone area may lead to design or retrofit of irregular structures without a clear view of their possible response. This study can be useful as drift damage is a main consideration for any seismic hazard analysis. The results can be useful to the insurance companies, governmental authorities, consultants, owners, and financial institutes.

Brief review of the selected model

This drift study emphases on the drift response of selected LRC frames with vertical and/or plane irregularities in low seismic zones with focusing on the Eastern and Northeastern parts of the US. The effect of low seismic instigation on LRC structures with vertical and/or plane irregularities is discussed here. The selected models are two (2), four (4), and eight (8) story frames, under three main families: BASE models without any irregularity, SYMETRIC models with the first tall story irregularity, and ASYMMETRIC models with the first story plan irregularity that may or may not have the first story elevation irregularity. The designated abbreviations for each group are letter B for Base, S for Symmetric and A for Asymmetric condition accordingly. The digit before the designated letter illustrates the number of levels, while the number after the designated letter denotes the first story height per foot measure. For example, model 4S18 means 4 story symmetric plan model which its first level has 18 feet (5.49m) height. To study plane irregularity similar to the typical construction in the US, the central columns are eliminated. A brief review of the static analysis assumptions, material and sections, and selected models is explained by Rezavandi and Fu [6].

Nonlinear Time History Analysis (THA) is executed using a step-by-step integration to compute the results. Nonlinear assumptions and methodology are according to FEMA 356 [1] procedure. Nonlinear computer software SAP 2000 [11] is used to perform analytical procedure and to obtain the drift results.

The drift response of LRC structures is done by considering relative story displacement, drift of the models. Story drift is one of the most practical and relevant measurements in the seismic design and studies of irregular structures. ASCE 41-06 [10] defines drift as "Horizontal deflection at the top of the story relative to the bottom of the story." In this study, acceptable structural performance levels and damages regarding drift is mentioned. These criteria are according to FEMA 356 [1] and ASCE 41-06 [10] for concrete frame structures.

Nonlinear Assumptions for Selected Models

To study dynamic response of the models, masses are allocated at all floor levels. The two nonlinearities of each THA case are (1) the first nonlinear step is P-A and then, (2) the final P-A state comprises the initial nonlinear condition for the gravity load according to FEMA 356 [1] requirements. Super position method cannot be used for nonlinear procedure, and former steps cannot be directly combined in THA response. Thus, the final step of nonlinear gravity combination acts as the initial state of any nonlinear THA analysis respectively. By this way, effect of gravity load would be effectively addressed.

Time history records selection

To select ground motions, PEER seismic database, Beta version, is used [12]. The concept of spectrum matching is the basis of PEER scaling approach, and assumptions and selected data are described in another paper [6]. One of the parameters in the target spectrum method is the period range or period interval. NEHRP [13] recommends to imply interval between 0.2T (minimum) and 3T (maximum) for moment frame buildings where T denotes the lesser (or greater) of the first mode translational periods along the two main horizontal axes of the structure. In this study, the period range is selected according to the median of the selected models, i.e. the four (4) story basic model (4B12), which are [0.348s, 5.37s]. By using PEER database [14], three pairs of records are chosen: Whittier Narrows (WNA), Loma Prieta (LPR), and Northridge (NOR). The selected records are from specific stations that provide required and requested scaling criteria. Each selected record is divided into two parts, Fault Normal (FN) and Fault Parallel (FP) that represent two perpendicular wave directions. 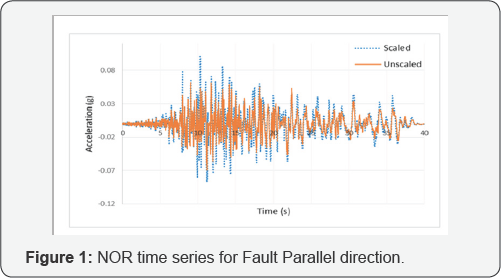Table 1 lists information of the selected scaled records and Figurel shows both scaled and unscaled accelerations against time series for NOR (FP of record sets).

The last record set is an unscaled record from PEER web application database [14] to intrinsically satisfy the Eastern region seismic condition as much as possible. The 1985 Nahanni (NAH) earthquake is suggested for a typical event of an East Coast US earthquake [15]. Furthermore, it is worthwhile to mention that selecting and scaling a different set of records for a group of structures are difficult, because they have a varied range of first mode periods [16]. Thus, the NAH earthquake is not scaled with the spectral matching method. To scale NAH record, the direct scale method is applied [17].

*: Results from PEER Ground Motion Database Search Criteria
**: Applied as direct linear scale factor (Maximum Scaled PGA)

Plastic hinge definition and allocation to models

For nonlinear study, the lumped plastic hinge model and backbone curve is the selected method. Concentrated hinge models may typically be suitable for simulating nonlinear response of columns and beams in frame systems [18]. The FEMA 356 [1] procedure and acceptance criteria are applied, and the software has the ability to calculate and comply the FEMA356 criteria [19]. Flexural plastic hinge is allocated to the beams in their strong directions. Flexural hinging of columns is assigned under the combined effects of bending in both directions and their interaction with axial loads. Shear failure is not explicitly included in the analysis models, but it is incorporated through the selected hinge failure modes and limitations per FEMA 356 [1] modeling parameters and acceptance criteria.

Hysteresis models for beams and columns

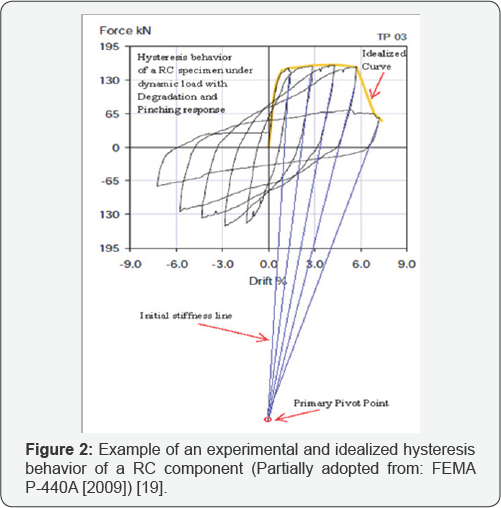
On RC columns, Elastic-Perfectly Plastic (Elasto plastic) hysteresis model is performed. Yavari et al. [20] compared the result of the RC frame model by using shaking table test and nonlinear analytical modeling. The tested RC moment frame consisted of columns, which were designed only for gravity loads. The acquired results by Yavari et al. [20] showed good compliance between the test and analytical models for Elasto plastic hysteresis model. Pivot hysteresis model [21] is used for the beams' hysteresis model. The experimental observations of RC members under cyclic or dynamic loads determine that majority of unloading paths are conducted toward a single point in a typical force-displacement (or moment-rotation) plane (Figure 2). This focal point is called the Pivot point [Ibid.]. To model LRC components, the Pivot model has several analytical advantages, namely pinching effect, degradation, hysteretic behavior verification through experimental observations, applicable to model unsymmetrical sections, and simplicity.

Damping model development

In the THA method, cyclic response of the plastic hinge is the framework of hysteresis damping. However, it is possible to induce some levels of artificial viscous damping forces in plastic hinges [22]. Consequently, overestimation of the damping ratio may cause errors in the calculation of the maximum nonlinear displacement of structures with intermediate to long period range. Oppositely, underestimation of the damping may lead to overestimate of displacements for shorter period ranges, specifically for less than 0.4 seconds [23]. On the other hand, by reviewing the result of the study by Dwairi et al. [Ibid.], it appears that the low ductile structures (such as LRC) show lower scatter in damping amount comparable with the higher ductile structural models.

In this regard, to calculate the viscous damping ratio, a simple equation is recommended by the PEER/ATC joint venture program [12]. This equation (Eqn. 1) is suitable for low to midrise buildings with less than 30 stories in which the maximum percent of critical damping (ξ) is defined as [Ibid.]:

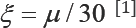
In Eqn. 1, n is a coefficient between 60 and 120 so that RC structures would likely be closer to the upper bound of |i coefficient [12] between 90 and 120. A reasonable damping ratio forn coefficient is assumed equal to arithmetic average of those limits, i.e. 105. Consequently, the damping ratio per Eqn. 1 would be equal to 3.5%.Using this method, all B and S archetype models are assumed to have critical damping ratio. For LRC structures with asymmetric plan, experimental results show that critical damping would be a reasonable estimate [24]. Thus, to acquire a suitable damping ratio for a LRC irregular plan structure located in low- to moderate- seismic zones, 2% damping ratio is applied which covers 2A12 through 8A18 models.

Hall [2006] developed a procedure to calculate linear viscous damping factors and this procedure is followed here. A in Eqn.2 determines bounds on the damping ratios within the specific frequency range, and R denotes the ratio of natural frequencies of the important modes [Ibid.].

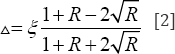
A classical viscous damping matrix, C, comprises of mass matrix, M, and stiffness matrix, K (Eqn.3):

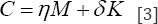
Hall [22] suggests that when the bound factor, i.e. A, is considerably low (relative to £], then n and Scan be calculated from the following equations:

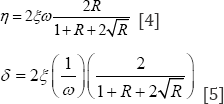
In Eqns.4 and 5, w indicates the first mode of vibration (rad/s); other terms have been defined previously. The computed factors would be performed to each associated model for nonlinear time history analysis in accordance with the software input requirements [11].

Applied dynamic analysis method

Each pair of scaled records consists of two separate load cases, FP and FN, which are applied for every single selected model. Thus, for each symmetric plan model, i.e. 2B12 to 8S18, total eight (4 x 2) different THA cases have been performed. For the irregular plan models, 2A12 to 8A18, the models are asymmetric in the North-South direction. Hence, an extra case of FP negative direction for each "A" model is performed to address this case.

The New mark method is the first choice of dynamic equation solver in this study. In case of instability and numerical issues, Hilber-Hughes-Taylor (HHT) is applied [19]. In the current study, for any THA case, which shows poor convergence, the new mark integration method has been shifted to the HHT procedure.

Analytical Result Review

Maximum Drift

In general, maximum (max.) drift may not only lead to structural damages, but also cause several problems interrelated to the serviceability of buildings, such as breakage of pipes and utility lines. Table 2 shows the maximum absolute drift (di) for the selected models which area acquired from the analysis results. Structural performance levels and damage criteria for vertical elements are presented in table C1-3 of FEMA 356 [1]. This table for concrete frames states that the maximum acceptable drift for Collapse Prevention (CP) is 4%, Life Safety (LS) 2%, and 1% is the acceptable range for Immediate Occupancy (IO). The absolute value of drift in the geometrical center of every story level (master point/joint) is attained. The two-, four-, and eight- story models are categorized into groups 1, 2, and 3, respectively. Two separate directions are presented for each group. Basically, the presented drift value associates with the maximum drift response among the four applied records for each model.

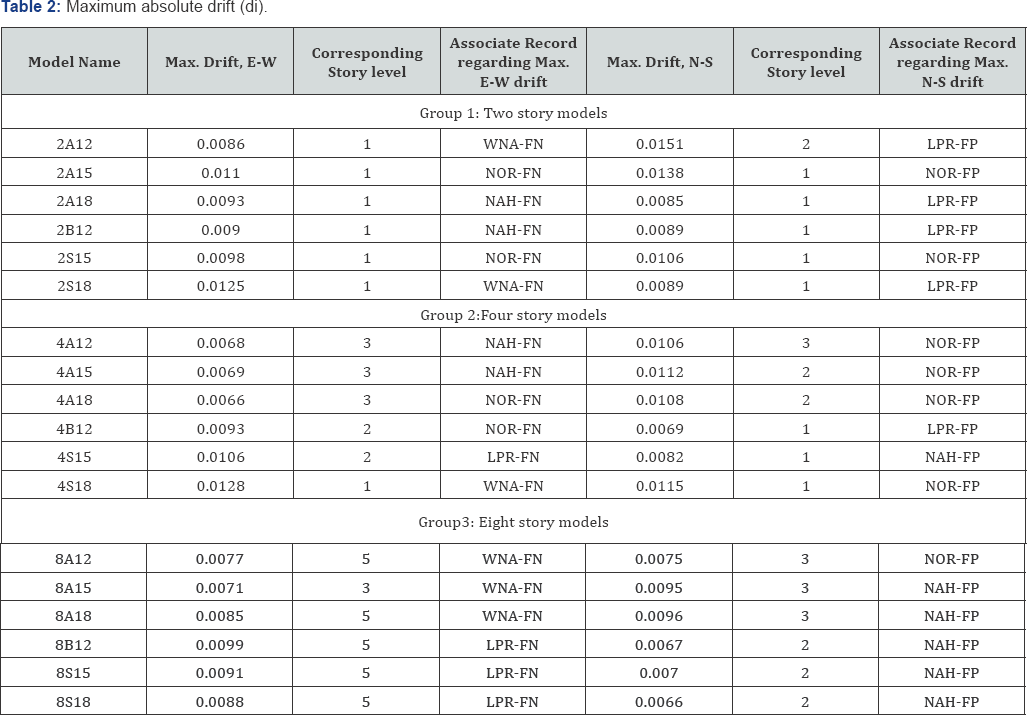
Expectedly, the maximum absolute drift for each direction is associated with the same direction of applied seismic records. From Table 2, the maximum amount of di is observed for 2A12 and 2A15 models in the N-S direction. 4S18 model has the most vulnerable condition in both N-S and E-W directions. However, the eight story models show overall less di in comparison with the other groups. In the E-W direction, di of group 2 and group 3 is mostly concentrated at the higher story levels while in the N-S direction the trend is reversed. For group 1, increase in the first story height shows low effect on di of regular plan models. For A type models of this group, the increase of the first story height may even lead to the reduction of di. For group 2, A type models are unaffected by the first story height alteration, but the first story height increment is induced higher value of di in the symmetric plan models. For the latter models, the maximum di is almost concentrated on the first story as well. Review of group 3 results reveals that there is no specific pattern for both asymmetric and symmetric plan models of this group.

Table 2 indicates that none of the models exceed FEMA 356 [1] LS performance criterion, although number of models, which suffers over IO drift damage level, is considerable. Table 2 also shows that there is no substantial difference between asymmetric plan and symmetric plan models in term of di. Moreover, it illustrates that eight (8) story models suffer less severe drift and their maximum drifts remain mostly within IO damage level. Numbers of upper and lower bounds of maximum drifts for both groups 1 and 2 with no difference between plan types are very similar and almost identical. For these groups, per FEMA 356 [1] drift criteria, each of these models under the applied records may encounter higher than IO level of damage.

Average drift

Although the maximum absolute drift may at least be attributed to LRC deficits, the proportionate drift change of all stories cannot be reflected properly. To compare and review the drift response of all selected models, the maximum drift result of each story level is acquired. In agreement with the selected Cartesian system (geometrical center of story level as the Cartesian center of the system), the drift response is collected with negative sign and positive sign for each direction of applied record. Then, the arithmetic mean of results (i.e. average of maximum drift of each story level under all applied records) for all seismic cases is calculated for negative and positive directions. To do so, every story level two cases regarding FN or FP component of the records (N-S or E-W) is computed independently. These results are illustrated in Figure 3-8. To study the effect of first story height on drift response, each figure comprises results for asymmetric or symmetric plan models. Both directions of seismic excitation (E-W or N-S) are depicted in independent diagrams. Average drift in both directions of oscillation (negative or positive) includes the horizontal axis and the story level shows the vertical axis of the diagrams.

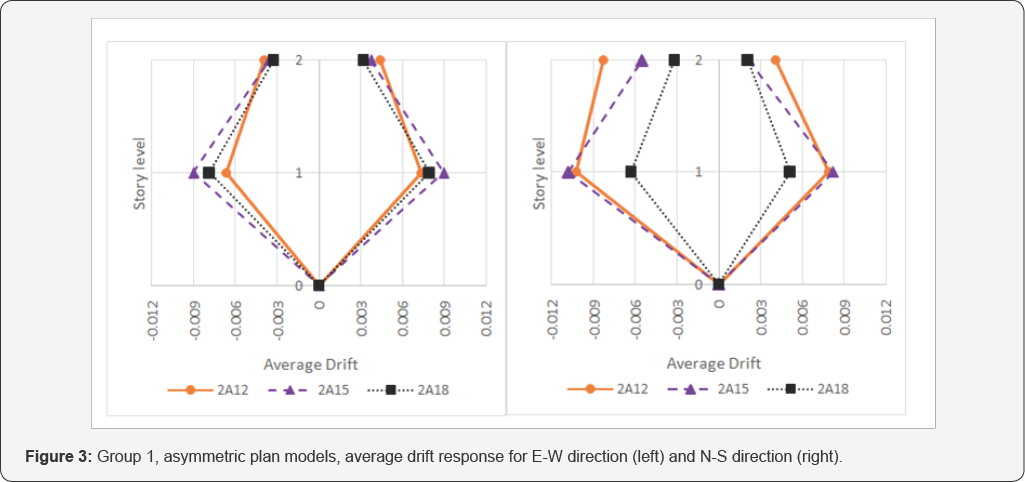
Overall, responses in figures 3 to8 are compatible with their effect on the drift response in comparison with the structural associated di in table 2. In other words, the inherent and specific dynamics behavior of the models. characteristics of the applied earthquakes may have lesser

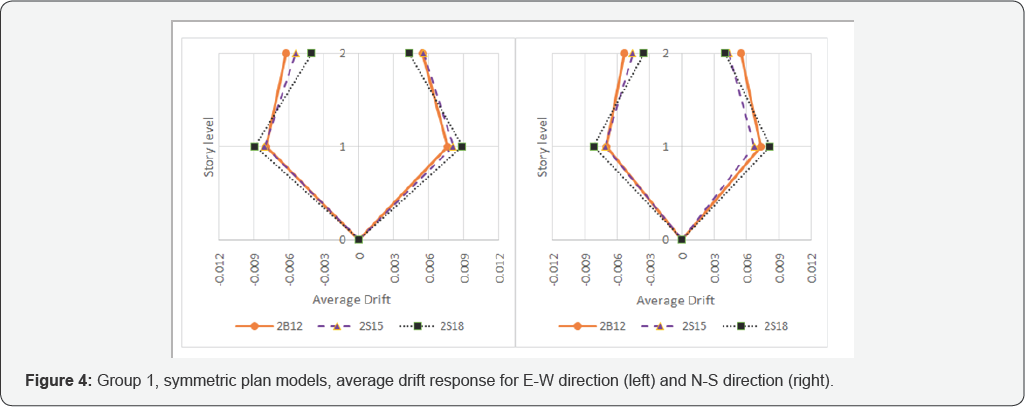
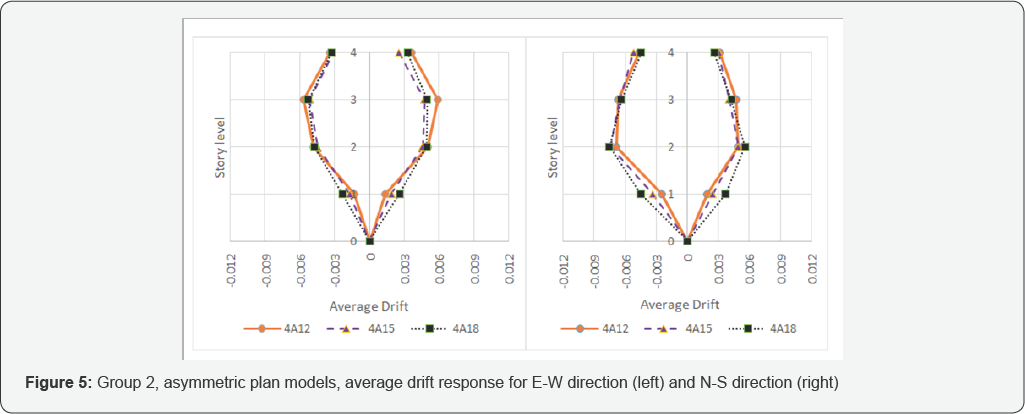
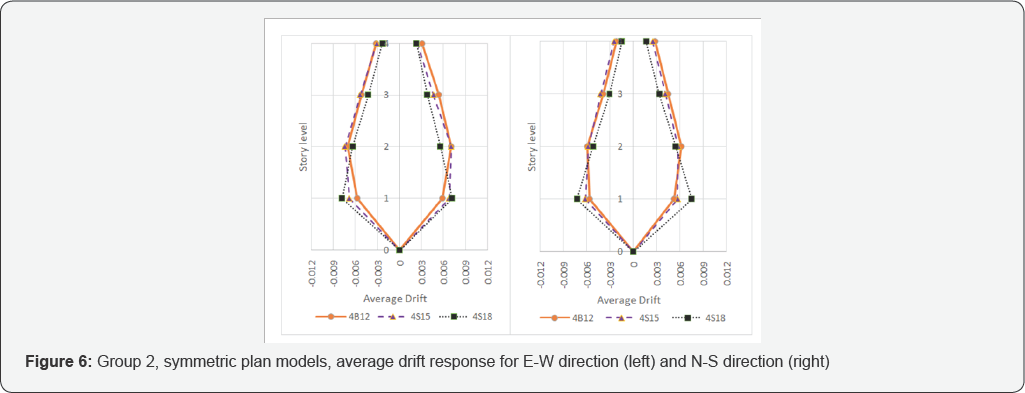
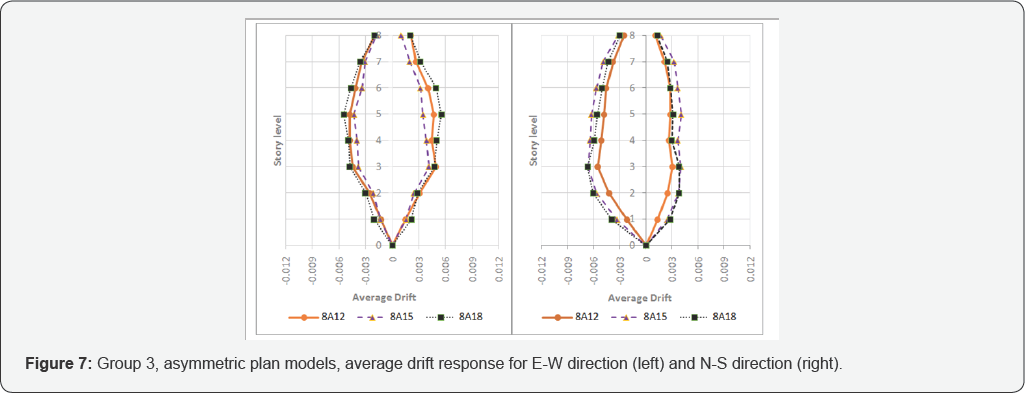
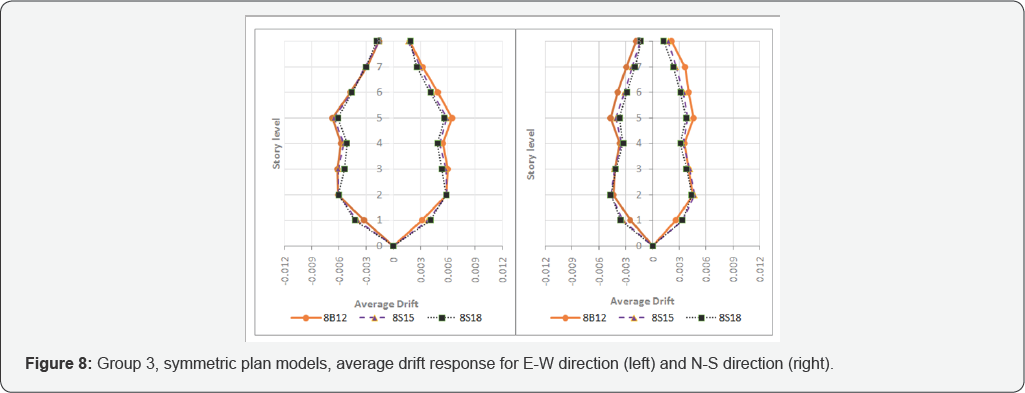
Figure 7 & 8 reveal that the average drift responses of eight story models are less than the other models. Regardless of the first story height, the N-S direction of asymmetric plan models show more average first story drift compared to the E-W direction. Lack of central columns in the first story at axis B (Frames 1 to 3, see Rezavandi and Fu) [6] is the most probable reason for this behavior. Archetype models 2A12 and 2A15 in the N-S direction suffer more than 1% average drift. Over IO drift level criterion is occurred only in the N-S direction at the first story level of the abovementioned models. Owing primarily to the higher level of hinge formations [Ibid.], these models suffer more lateral deformation. None of the other selected models goes beyond the FEMA 356 [1] IO damage level although results show light sparse.

Four (4) story asymmetric plan models have the same column section for their first story level. This is also the case for the eight (8) story asymmetric plan models, which are obtained through the traditional linear static analysis and design approach. Average drift response of the first story of these models shows a typical sequence. It means by increasing of the first story height for each group of models with taller first stories induces more drift value. As mentioned, the column sections are the same, and the previous sequence is occurred for both E-W and N-S directions. Thus, these can only be explained by considering soft story possibility, although in this case the acquired drift is far less than story mechanism level. Furthermore, difference between the E-W responses for all of these models is less in contrast with the N-S direction (Figure 5 & 7). This shows the effect of central column elimination on the average drift response. For the aforementioned models, the response of upper stories do not show any specific trend and more drift is observed for all those models in upper stories than the first story. Due to the facts that the input excitations (the applied THAs) for all of these cases are the same, [25] material and structural sections for all of the abovementioned models are similar (despite the inherent similar dynamic analysis approach) this complex phenomena in upper levels may only be associated with the irregular shape of these models.

The previous trend is attributed to symmetric plan models; i.e. models with taller first story, namely with 4.57m (15 feet) or 5.49m(18 feet) first story height, show more first story drift. However, the first story column section is not similar for this group of models. In fact, 4S15 and 4S18 models have similar first story column section while model 4B12 has a smaller section. Additionally, models 8B12 and 8S15 have similar first story section while the column section of model 8S18 is different in this case. Similarity of the first story average drift between the symmetric and asymmetric plan models shows that the vertical irregularity may involve more in the erratic upper stories response than the plan irregularity. In agreement with the above statement, Figure 6 is addressed. In this figure, which is for group 2 models with symmetric plan, both principal directions of model 4S18 response depict more drift concentration on the first story. This case is a classical condition of susceptible soft story response. 4B12 model is more regular while 4S15 model behaves between 4S18 and 4B12 models with bias toward 4B12 drift response than 4S18. Though the vertical irregularity effect in particular and overall drifts response in general is less dominant for the eight story models, this is also the case for eight story models with regular plan (Figure 8).

Figure 3-8 are categorized based on the similarity in both of the number of stories and the first story plan type. To get a better view from the preceding results and to review the effect of number of stories on the response, the same average drift results are presented according to story height similarity. In this case, figures 9 to 11 are provided to show the average drift for models with the first story heights equal to 3.66 m, 4.57 m, and 5.49 m (12, 15, and 18 feet), respectively. These figures may also be used to compare the plan irregularity effect on the response of the models.

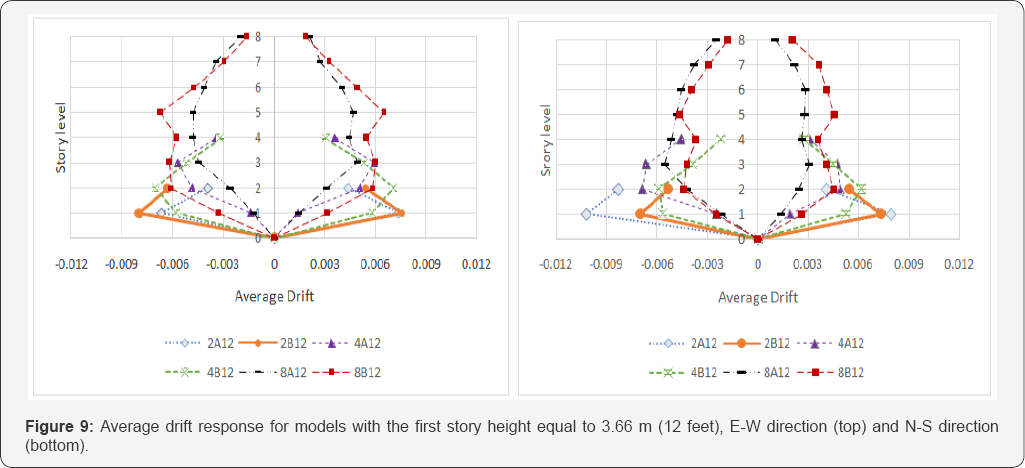
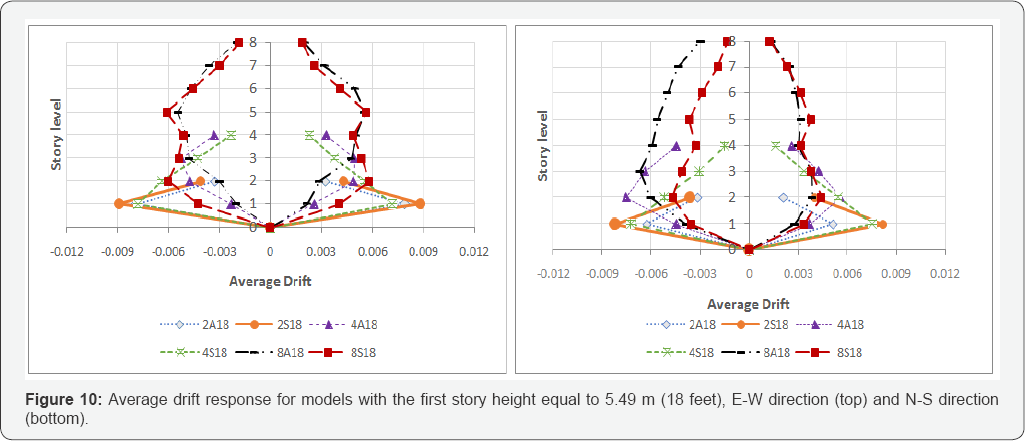
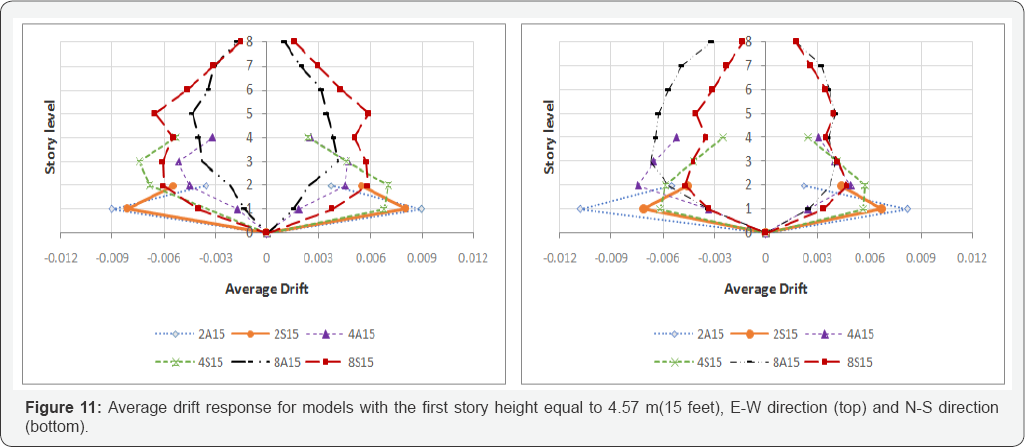
Unequivocally, the same result regarding lesser average drift for eight story models in comparison with four story models is observable in the following figures. The same trend is clear for the comparison of four story models with the two story models.

Review of eight story models response shows their response is attributed to the elastic stiffness. In addition, the archetype models are originally designed for dead and live load effects. The structural members for A type models are heavier than the symmetric plan models, specifically in the first two stories. The stiffer lower story levels of model 8A12 in the E-W direction (Figure 9, top) have less average drift in comparison with the 8B12 model in its lower stories. Their response gets closer in the upper stories.

8A18 model also has less average drift at its first story than 8S18 while the difference between 8A18 and 8S18 becomes mostly closer in lower levels. Again, the possible soft story phenomenon may be prominent in this case. Models with 5.49m (18 feet) first story height illustrate higher level of erratic response than 4.57m (15 feet) first story height models.

For the abovementioned models, responses of models 8A18 to 8S18 are very close for the positive part of the N-S direction (Figure 10, bottom). It is the case for models 8A15 and 8S15 in Figure 11 (bottom). The possible reason for this behavior is the presence of strong frame in axis 4 of asymmetric plan models, which help to absorb the seismic energy (movement) elastically. In the negative direction of applied seismic, less stiff part of the frame system (lack of middle column line) leads to increase in the overall responses of models 8A18 and 8A15 in contrast with the 8S18 and 8S15 models. The difference between average drift for models 8A12 and 8B12 becomes much less in the negative part of N-S direction. It means the weak part of stiffness irregularity (in plan) causes more drift in its side (which may be achievable in elastic analysis as well), but the elevation irregularity can exacerbate the drift response considerably.

To do the same analogy, overall responses in the E-W and N-S directions of four (4) story models are very similar to the former responses of eight story models. In this case, the difference between responses is sharper than for eight story models. Almost all asymmetric four story models have less drift in their first story than the symmetric plan models. The results get closer or reverse for higher levels. The lower columns and beams in asymmetric four story models are stronger than corresponding symmetric models. All four story selected models have similar column section at levels above the first level. Thus, the response becomes closer toward upper levels. The effect of first story height does not illustrate any specific trend for this group of models.

Two story models have more drift while their response is more sporadic in comparison with other models. (Figure 9 & 11) show that 2A12 and 2A15 models have more or at least very close average drift corresponding to their symmetric plan models.

Conclusion

Except for few models, the eight story models show less maximum absolute drift in comparison with the other models. THA analysis shows that the maximum absolute drift for all eight story models are within IO damage level per FEMA 356 [1] criteria. Four and two story models may suffer more drift, although their maximum drifts do not reach LS level. For the latter models, low intense seismic event may impose noticeable damage state in LRC structures. Regardless of symmetric or asymmetric plan configuration, the maximum absolute drift is independent to the input records for two and four story models, versus eight story models in which input record is the dominant parameter for the acquired maximum absolute drift.

The maximum absolute drifts for both plan and/or vertical irregular structures of this study do not show considerable difference. This result is in disagreement with most design code interpretations and assumptions regarding higher expected drift value for a structure with both plan and height irregularities. Maximum average drift reveals that the structural dynamic behavior may affect response more than the inherent characteristics of applied ground motions.

Lack of the first story middle row column for asymmetric plan model causes more drift in the N-S directions comparing to the E-W direction of the same models. Irregularities of the models affect the models' drift response in their higher story levels. Models with more irregularities (i.e. both plan and vertical irregularities) illustrate more erratic drift response in their upper levels than models with one irregular condition. The structural member size in lower stories has considerable effect in the maximum average drift response in the lower stories. For asymmetric plan models, the direction of excitation (in the N-S axis) affects the maximum average drift response.

Increase of the first story height shows negligible and even reverse effect to the maximum absolute drift for most asymmetric plan models. Similar to symmetric plan models, the maximum average drift values for eight and four story models are increased through increment of the first story height. Additionally, similar to the previous conclusion, the same possible soft story influence on the maximum average response is recognizable for these cases as well.

While, there is a general agreement on hazardous effect of plan irregularity corresponding to drift response in high seismic zones, (Figure 3-11) show that there might be considerable disagreement in this case regarding selected models of this study. These figures illustrate that the taller models suffer less drift, and asymmetric plan in the first story does not change the overall response significantly. Indeed, for several conditions, the plan irregular models illustrate lower amount for average drift. However, consequence of the first story height still affects the drift response of the selected models.

Within maximum drift results and outcomes of the selected models, it is clear that low intense seismic events may create a degree of noticeable damages in LRC structures. The damage level is more for low-rise structures in comparison with the taller models. Per seismic design regulations in most building codes, e.g. ASCE 7-10 [7], it is expected to see higher damage level for asymmetric plan structures. The unsymmetrical plan models indicate almost similar drift performance in comparison with the symmetrical plan models regarding maximum drift criterion.

Within the framework of this study, design of structural members per early edition of design codes, without any seismic consideration, seems to be sufficient to withstand the applied ground motions regarding drift requirements. Failures do not seem to occur for structural members with vertical irregularities, while extreme vertical irregularity is applied for selection of the first story height. It seems like that the more strict requirements of ASCE 7-10 [7] with regard to vertical irregularities are mostly applicable for high seismic zones. However, damage due to drift can be dominant for an irregular structure in a low seismic zone, as the damage level is not ignorable as shown before.

The current study shows that more attention may be required by the authorities and professional societies to the drift effect. While low seismic zone is a colloquial term, that does not mean a zero damage. Indeed, lack of enough records and ignorance of seismic design requirements in the existing LRC buildings, in low to moderate seismic zones, can end up to an unexpected damage level during a seismic event.

For More Open Access Journals Please Click on: Juniper Publishers

Fore More Articles Please Visit: Civil Engineering Research Journal