The Implication of Analysis Module on Vehicle Bridge Interaction Modelling- Juniper Publishers

Juniper Publishers- Journal of Civil Engineering

Abstract

Bridge structures are susceptible to devastating failures ascribing to the continuous strength reduction over time, as well as the unprecedented increase in freight volumes. Therefore, understanding the dynamic response of bridges due to moving traffic, specifically heavy trucks, has attracted the interest of the highway engineers. To this end, Vehicle Bridge Interaction (VBI) modelling has been adopted as a reliable and effective approach to mimic bridge vibrations under transit traffic. The decoupled VBI modelling is based upon solving the vehicle and the bridge equations of motion separately, by equating the contact forces between the vehicle and the bridge at each time step. The equations of motion can be solved either implicitly or explicitly. Implicit analysis directly solves for the displacement vector {x}, which consequently requires calculation of inverse of stiffness matrix. Whilst explicit analysis solves for the acceleration vector {x} by inverting the mass matrix. Most of VBI algorithms adopt an implicit solver, however, the implicit analysis is adequate to simulate static and quasi-static responses which is not representative of the dynamic nature of the truck and bridge vibrations in the field. This article is devoted to illuminate the difference between explicit and implicit solvers in modelling the VBI problems. The implicit modelling was implemented in MATLAB, while the explicit solution was performed using LS- Dyna FEA program. The study pay off is to high light the implication of the solver module on the modelling results which could be essential for some applications specifically when the faint changes in the bridge responses are of interest, such as Bridge Health Monitoring and Drive-by Bridge Inspection applications.

Introduction

The degradation in the structural integrity of the highway bridges is ascribing to ageing and the dramatic increase in freight volumes. In the United States, approximately 11% of the bridges on the transport network has been classified as structurally defective [1,2]. Therefore, bridge safety assessment under operational traffic weight has become an essential area of research [3-5]. To this end, it is imperative to depict the bridge attribute (real time vibration) under the weight of passing vehicles [6,7]. To simulate the vehicle bridge interaction, one of the following approaches can be adopted [6,7],

a. Decoupling the vehicle and the bridge equation of motions and solving their equations independently by equating the contact forces between the vehicle and the bridge in an iterative procedure [8,9], or
b. To couple the vehicle and the bridge equation of motions by eliminating the contact force from their equations and having one system matrix includes the vehicle and the bridge properties [10,11]. These concepts are based upon achieving equilibrium of forces and compatibility of displacements at the point of contact between the vehicle and the bridge during the simulation time. In short, either of these concepts can be followed to link the vehicle and the bridge equations of motion as depicted in (Figure 1). The resulted equations represent the Vehicle Bridge Interaction (VBI) system. The equations of motion in the VBI system can be either solved implicitly or explicitly as previously noted. Implicit analysis, which is widely used in civil engineering applications, is based upon solving the displacement vector {x}, then calculate its derivative to estimate the velocity and the acceleration. Consequently, it requires inverting the system stiffness matrix which is often a complex procedure and in some cases requires a numerical solver to invert the matrix once or even several times over the time step. On the other hand, the analysis is unconditionally stable and is independent of the size of the time step [8,12]. In another vein, the explicit analysis solves the acceleration vector {x "} rather than the displacement vector {x}, hence it is accompanied with inverting the diagonal mass matrix. Therefore, the inversion step in the explicit analysis is not an expensive operation, however, the time step must be less than the Courant step (time it takes a sound wave to travel across an element), which results in a discrete time step. Explicit analysis manifests in highly transit dynamic analysis, such as explosions, impact and crash analysis. Vehicle Bridge Interaction modelling can be classified as highly transit dynamic problem, unlike other civil structures, where a massive dynamic load used to traverse the bridge in a fraction of a second (e.g. a vehicle travelling with 27m/s [60mph] will cross a 10m bridge in 0.37sec). Accurate representation for the bridge vibration is imperative for bridge Health Monitoring applications, especially that SHM techniques rely on observing the anomalies in the structure response which are associated to the presence of damage [5,13]. This article highlights the effect of the analysis technique on the vehicle and the bridge responses. The implicit analysis has been carried out using MATLAB VBI algorithm [14-16]. Whilst, the explicit modelling of the VBI problem has been performed with the aid of LS-Dyna FE program. The goal of this article is to discuss the plausibility of using implicit analysis to solve the VBI problem, specifically for Bridge Health Monitoring applications.

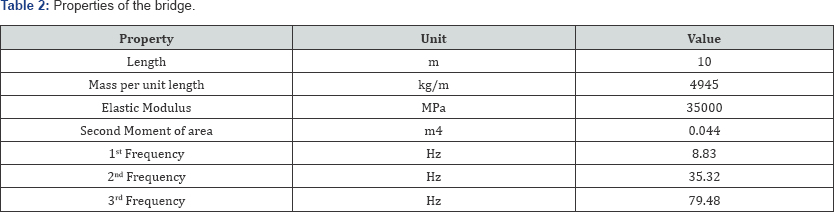
Vehicle and Bridge Properties

The vehicle has been modelled as a quarter car with two degrees of freedom, the axle mass and body mass translations. The vehicle model is shown in Figure 1 and its properties are based on the works of Cebon [17] and Harris, O Brien and Gonzalez [18]. A 15-m bridge will be utilized in this study. The bridge properties are shown in Error! Reference source not found.

Comparison between Implicit and Explicit Solvers Results

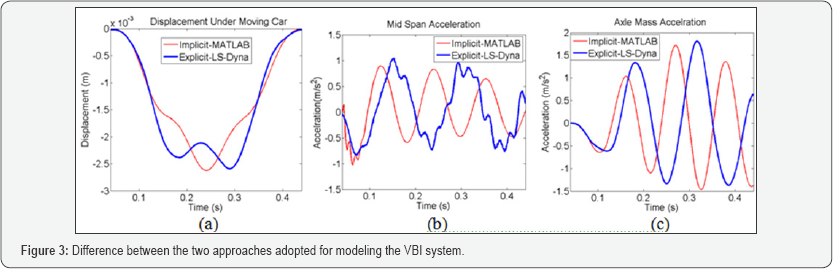
The quarter car model has been simulated crossing the 10-m bridge, and the analysis has been carried out twice using explicit and implicit analysis (Figure 2) (Table 1). Figure 3 illustrates the results of the mid-span acceleration, the Quarter-car axle mass acceleration history and the displacement under the passing quarter car for the two modules. The first point of note, is that there is a dramatic difference between the two attributes. The amplitude of the responses (i.e. for all the figures) are closely matched, however, the response shape is completely different. First, explicit module showed two bouncing in the displacement history (Figure 3a), while the implicit analysis shows an attribute close to the static responses of the bridge. The results are deemed to be compelling with the nature of the implicit and explicit solvers. The implicit solver is adequate to represent low-frequency vibration responses, this clearly depicted in the bridge displacement which tends to be static. On the other hand, the discrete time step of the explicit analysis allows capturing the incremental changes in the bridge vibration over the sample time. Similar behaviours are found for the acceleration of the bridge midpoint (Table 2). Figure 3b & 3C shows that implicit solver gives a pure sinusoidal signal, while the explicit solver shows some perturbation around the mean value. The quarter- car responses are shown to be similar, yet still not identical for the two cases.

Conclusion

This article high lights the difference between implicit and explicit analysis in simulating Vehicle Bridge Interaction problems. The authors presume that explicit analysis is preferable for modelling VBI problems. The small size of the step allows for municipal vibrations to be depicted for each point along the bridge. This is essential for bridge health monitoring applications since those techniques are based upon tracking the changes in the bridge responses due to the presence of damages. The results listed in this article showed the dramatic difference between the two solvers, which requires further investigation to ascertain the solver's suitability for vehicle bridge interactions modelling.

Acknowledgement

The authors wish to express their gratitude for the financial support received from the National Science of Foundation (NSF- CNS-1645863). Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the authors and do not necessarily reflect the view of the sponsors.

For More Open Access Journals Please Click on: Juniper Publishers

Fore More Articles Please Visit: Civil Engineering Research Journal